CF2041N Railway Construction

Truckski 国位于一个崎岖的山区，地质条件导致了许多问题。复杂的地形将国家内的不同州分隔开来，导致州际通行极为不便，更重要的是缺乏中央政府的有效控制。此外，犯罪率逐年上升，严重影响了无辜公民的日常生活。 最近的一次抗议终于让这一情况引起了重视，新当选的总统宣布了一项雄心勃勃的计划来解决这些问题。她的计划包括两个主要部分。第一部分是在各州之间修建高速铁路，以促进全国的联系和团结。由于各州大多独立运行，若要在州 $u$ 和州 $v$ 之间修建铁路，政府需要支付 $a_u + a_v$ 美元，其中 $a_u$ 美元支付给州 $u$，$a_v$ 美元支付给州 $v$。铁路为双向通行，即建成后，州 $u$ 和州 $v$ 的居民可以互相往来。几乎任意一对州之间都可以修建铁路，除了 $m$ 对特殊的州，由于地形极其险峻，无法直接修建铁路。 计划的第二部分是在全国范围内建设一个集中管理所有罪犯的中央监狱。鉴于预计囚犯数量众多，总统决定选择一个州来建设中央监狱，并将该州与其他所有州的联系切断。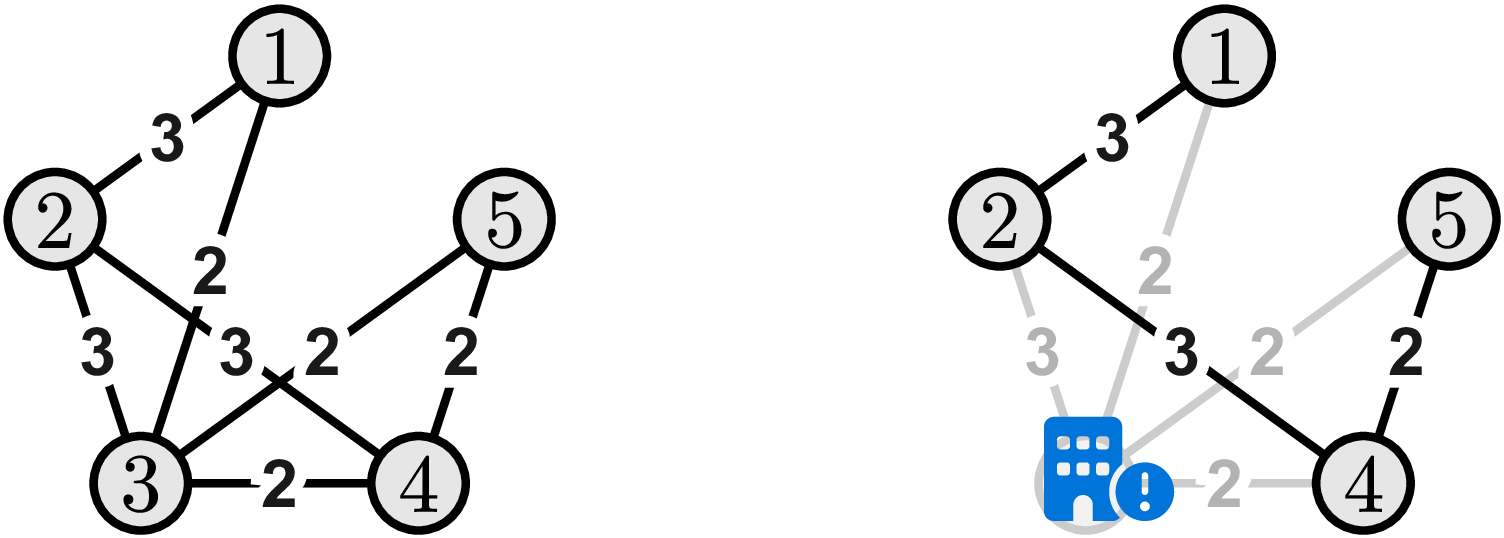  样例输入 1 的示意图。（a）为各州之间直接修建铁路的费用。（b）考虑在第 3 州建设中央监狱。所有不涉及第 3 州的直接铁路都需要修建，总费用为 $3+3+2=8$ 美元。 基于上述情况，总统希望寻找一份最低成本的铁路建设方案，使得： - 建有中央监狱的州不应与任何其他州有铁路相连； - 其余所有州应当连通，即任意两个这样的州之间都可以通过一条或多条铁路互相到达。 你作为总体规划团队的一员，需要在几个小时后的会议上向总统汇报不同建设方案的成本。请你计算，对于每一个州 $u$，当中央监狱建在 $u$ 州时，满足上述条件的铁路建设的最小成本。

输入的第一行包含两个整数 $n$ 和 $m$，分别表示 Truckski 国的州数和无法修建铁路的州对数。下一行包含 $n$ 个整数 $a_1, \ldots, a_n$，其中 $a_i$ 表示政府需要支付给第 $i$ 个州的建设费用。接下来的 $m$ 行，每行包含两个整数 $u_i$ 和 $v_i$，表示无法在州 $u_i$ 和州 $v_i$ 之间直接修建铁路。 - $2\leq n\leq 10^5$ - $0\leq m\leq 10^5$ - $1\leq a_i\leq 10^9$ - $1\leq u_i

输出一行 $n$ 个整数，第 $i$ 个整数表示当第 $i$ 个州作为监狱建设地时，满足条件的铁路建设的最小成本。如果不存在可行的铁路建设方案，则输出 $-1$。

由 ChatGPT 4.1 翻译