CF2042E Vertex Pairs

给定一个由 $2n$ 个顶点组成的树。回想一下，树是一个没有环的连通无向图。每个顶点上都写了一个从 $1$ 到 $n$ 的整数。从 $1$ 到 $n$ 的每个值都恰好写在两个不同的顶点上。每个顶点也有成本，顶点 $i$ 成本 $ 2^i $。 你需要选择树的一个顶点子集，如下所示： - 子集是连通的；也就是说，从子集中的每个顶点，只通过子集中的顶点可达子集中的每个其他顶点； - 从 $ 1 $ 到 $ n $ 的每个值都至少写在子集中的一个顶点上。 在所有这样的子集中，您需要找到其中顶点的总代价最小的子集。注意，您不需要最小化子集中的顶点数量。

第一行包含一个整数 $ n $ （$ 1 \le n \le 2 \cdot 10^5 $）。 第二行包含 $ 2n $ 个整数 $ a_1, a_2, \dots, a_{2n} $ （$ 1 \le a_i \le n $）。从 $ 1 $ 到 $ n $ 的每个值恰好出现两次。 接下来的 $ 2n-1 $ 行中每行包含两个整数 $ v $ 和 $ u $ （$ 1 \le v, u \le 2n $）——树的边。这些边构成了一棵有效的树。

在第一行中，打印一个整数 $ k $ ——子集中的顶点数。 在第二行中，打印从 $ 1 $ 到 $ 2n $ 的 $ k $ 个不同整数——所选子集中顶点的索引。顶点可以以任意顺序打印。

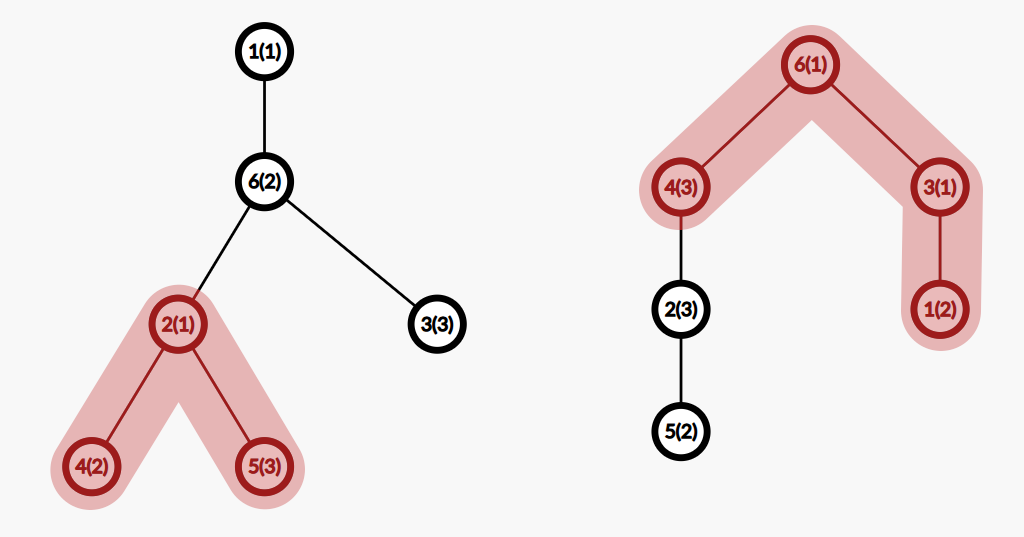The images show the answers to the first two examples. The numbers in parentheses are the values written on the vertices. In the first example, there are valid subsets such as: $ [2, 4, 5] $ (with a cost of $ 2^2 + 2^4 + 2^5 = 52 $ ), $ [2, 4, 5, 6] $ (with a cost of $ 116 $ ), $ [1, 6, 3] $ (with a cost of $ 74 $ ), $ [2, 6, 3] $ (with a cost of $ 76 $ ), and many others. In the second example, the cost of the subset $ [4, 6, 3, 1] $ is $ 90 $ .