CF2044H Hard Demon Problem

Swing 正在筹备他的煎饼工厂！一个优秀的煎饼工厂需要具备出色的压平能力，所以 Swing 决定使用二维矩阵来测试他的新设备。 给你一个大小为 $ n \times n $ 的矩阵 $ M $，其中每个元素都是正整数。Swing 有 $ q $ 个查询需要回答。 对于每个查询，Swing 会给出四个整数 $ x_1 $、$ y_1 $、$ x_2 $ 和 $ y_2 $，以此定义一个子矩阵，该子矩阵的左上角为 $(x_1, y_1)$，右下角为 $(x_2, y_2)$。他希望你将这个子矩阵展平为一个一维数组 $ A $。具体的展平顺序是：从 $ M_{(x1,y1)} $ 开始，按行从左到右依次加入子矩阵中的元素，直到 $ M_{(x2, y2)} $ 结束。 下图通过红色虚线展示了子矩阵的边界，橙色箭头指示了元素在进入数组 $ A $ 时的顺序，图下方展示了最终的数组 $ A $。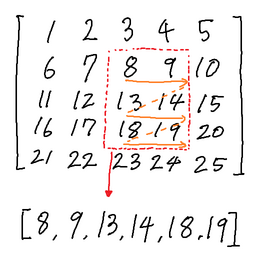  展平后，Swing 想知道 $\sum_{i=1}^{|A|} A_i \cdot i$ 的值，即数组中每个元素 $ A_i $ 乘以其下标 $ i $ 的总和。

输入的第一行是一个整数 $ t $（$ 1 \leq t \leq 10^3 $），表示测试用例的数量。 每个测试用例的第一行给出两个整数 $ n $ 和 $ q $（$ 1 \leq n \leq 2000, 1 \leq q \leq 10^6 $），分别表示矩阵的大小和查询的个数。 接下来的 $ n $ 行中每行包含 $ n $ 个整数，分别为矩阵 $ M $ 的元素 $ M_{(i,1)}, M_{(i,2)}, \ldots, M_{(i,n)} $（$ 1 \leq M_{(i, j)} \leq 10^6 $）。 接下来的 $ q $ 行每行包含四个整数 $ x_1 $、$ y_1 $、$ x_2 $ 和 $ y_2 $（$ 1 \leq x_1 \leq x_2 \leq n, 1 \leq y_1 \leq y_2 \leq n $），表示每次查询的边界。 确保所有测试用例中的 $ n $ 的总和不超过 $ 2000 $，$ q $ 的总和不超过 $ 10^6 $。

对于每个测试用例，输出 $ q $ 个查询的结果，每个结果单独占一行。

在第一个测试用例的第二个查询中，数组 $ A = [9, 5, 5, 2] $。因此，结果为 $ 1 \cdot 9 + 2 \cdot 5 + 3 \cdot 5 + 4 \cdot 2 = 42 $。 **本翻译由 AI 自动生成**