CF2044H Hard Demon Problem

Swing is opening a pancake factory! A good pancake factory must be good at flattening things, so Swing is going to test his new equipment on 2D matrices. Swing is given an $ n \times n $ matrix $ M $ containing positive integers. He has $ q $ queries to ask you. For each query, he gives you four integers $ x_1 $ , $ y_1 $ , $ x_2 $ , $ y_2 $ and asks you to flatten the submatrix bounded by $ (x_1, y_1) $ and $ (x_2, y_2) $ into an array $ A $ . Formally, $ A = [M_{(x1,y1)}, M_{(x1,y1+1)}, \ldots, M_{(x1,y2)}, M_{(x1+1,y1)}, M_{(x1+1,y1+1)}, \ldots, M_{(x2,y2)}] $ . The following image depicts the flattening of a submatrix bounded by the red dotted lines. The orange arrows denote the direction that the elements of the submatrix are appended to the back of $ A $ , and $ A $ is shown at the bottom of the image. 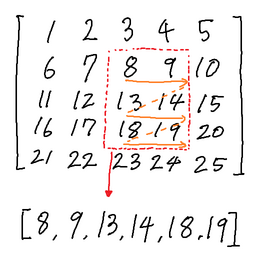Afterwards, he asks you for the value of $ \sum_{i=1}^{|A|} A_i \cdot i $ (sum of $ A_i \cdot i $ over all $ i $ ).

The first line contains an integer $ t $ ( $ 1 \leq t \leq 10^3 $ ) — the number of test cases. The first line of each test contains two integers $ n $ and $ q $ ( $ 1 \leq n \leq 2000, 1 \leq q \leq 10^6 $ ) — the length of $ M $ and the number of queries. The following $ n $ lines contain $ n $ integers each, the $ i $ 'th of which contains $ M_{(i,1)}, M_{(i,2)}, \ldots, M_{(i,n)} $ ( $ 1 \leq M_{(i, j)} \leq 10^6 $ ). The following $ q $ lines contain four integers $ x_1 $ , $ y_1 $ , $ x_2 $ , and $ y_2 $ ( $ 1 \leq x_1 \leq x_2 \leq n, 1 \leq y_1 \leq y_2 \leq n $ ) — the bounds of the query. It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 2000 $ and the sum of $ q $ over all test cases does not exceed $ 10^6 $ .

For each test case, output the results of the $ q $ queries on a new line.

In the second query of the first test case, $ A = [9, 5, 5, 2] $ . Therefore, the sum is $ 1 \cdot 9 + 2 \cdot 5 + 3 \cdot 5 + 4 \cdot 2 = 42 $ .