CF2045E Narrower Passageway

你是 ICPC 王国的一名战略家，近日你收到情报，王国附近的一条狭窄通道将遭遇怪物的袭击。这条通道可以简化为一个 2 行 $N$ 列的网格。我们用 $(r, c)$ 表示网格中第 $r$ 行第 $c$ 列的格子。每天会安排一个力量值为 $P_{r, c}$ 的士兵驻守在 $(r, c)$ 位置上。 这里常年大雾，每列都有 $50\%$ 的概率被雾气笼罩。一旦某列被雾气覆盖，两个驻守该列的士兵将无法执行任务。否则，士兵将正常部署。 我们定义一个连通区域 $[u, v]$（$u \leq v$）为从第 $u$ 列到第 $v$ 列连续且无雾的列。下面的示例中，灰色部分代表被雾覆盖的格子，共有四个连通区域：$[1, 2]$、$[4, 6]$、$[9, 9]$ 和 $[11, 11]$。  连通区域 $[u, v]$ 的力量可以这样计算。设 $m_1$ 和 $m_2$ 分别为该区域内第一行和第二行士兵力量的最大值。具体来说，对于 $r \in \{1, 2\}$，有 $m_r = \max (P_{r, u}, P_{r, u + 1}, \dots, P_{r, v})$。如果 $m_1 = m_2$，则该区域的力量是 $0$；否则，力量为 $\min (m_1, m_2)$。 一个工作日的总力量定义为所有连通区域力量的总和。请计算在任意一天部署的期望总力量。

第一行是一个整数 $N$，表示列数（$1 \leq N \leq 100\,000$）。 接下来的两行，每行包含 $N$ 个整数，表示士兵的力量值 $P_{r, c}$（$1 \leq P_{r, c} \leq 200\,000$）。

设 $M = 998\,244\,353$。可以证明期望总力量表示为一个不可约分数 $\frac{x}{y}$，其中 $x$ 和 $y$ 是整数，且 $y \not\equiv 0 \pmod{M}$。请输出一个整数 $k$，使得 $0 \leq k < M$ 且 $k \cdot y \equiv x \pmod{M}$。

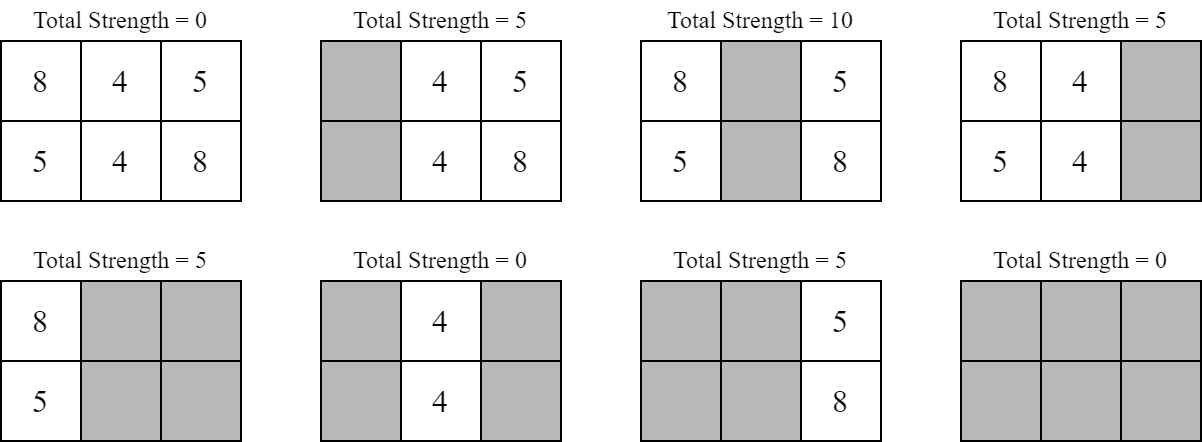
样例输入/输出 #1 解释 这条通道可能有 $8$ 种不同的布局。  每种布局出现的概率是相同的。因此，期望总力量为 $(0 + 5 + 10 + 5 + 5 + 0 + 5 + 0) / 8 = \frac{15}{4}$。由于 $249\,561\,092 \cdot 4 \equiv 15 \pmod{998\,244\,353}$，所以样例的输出为 $249\,561\,092$。 样例输入/输出 #2 解释 期望总力量为 $\frac{67}{16}$。 **本翻译由 AI 自动生成**