CF2045L Buggy DFS
题目描述
你正在学习一种名为深度优先搜索(DFS)的图遍历算法。然而,由于一个小错误,你的算法与标准版本略有区别。以下是你实现的有误深度优先搜索(BDFS)算法,假设图中有 $N$ 个节点(编号从 $1$ 到 $N$)。
```
BDFS():
令 S 为一个空栈
令 FLAG 为大小为 N 的布尔数组,初始值均为 false
令 counter 为一个整数,初始化为 0
将 1 压入栈 S
当 S 不为空时:
弹出 S 的栈顶元素到 u
FLAG[u] = true
对于 u 的每个邻居 v(按升序访问):
counter = counter + 1
如果 FLAG[v] 为 false:
将 v 压入栈 S
返回 counter
```
你发现这个错误让算法比标准的 DFS 慢。通过查看函数 BDFS() 的返回值可以探究这个问题。为了更好地研究算法的行为,你打算构造一些无向简单图,让函数 BDFS() 的返回值等于 $K$,或者确定这样的图是否存在。
输入格式
输入只包含一个整数 $K$ ($1 \leq K \leq 10^9$)。
输出格式
如果无法构造一个无向简单图使得 BDFS() 返回 $K$,则输出 -1 -1。
否则,按照以下格式输出图的描述。第一行包含两个整数 $N$ 和 $M$,分别表示图中的节点数和无向边数。接下来的 $M$ 行,每行包含两个整数 $u$ 和 $v$,表示连接节点 $u$ 和节点 $v$ 的一条无向边。边的顺序可以随意,图需满足以下条件:
- $1 \leq N \leq 32\,768$
- $1 \leq M \leq 65\,536$
- 对于所有的边,$1 \leq u, v \leq N$
- 图为无向简单图,即没有重边和自环
注意,你不需要尽量减少节点或边的数量。可以证明,如果可以构造一个图使得 BDFS() 返回值为 $K$,则必然存在一个满足所有上述限制条件的图解。若有多个解,任选其一即可。
## 例子与提示
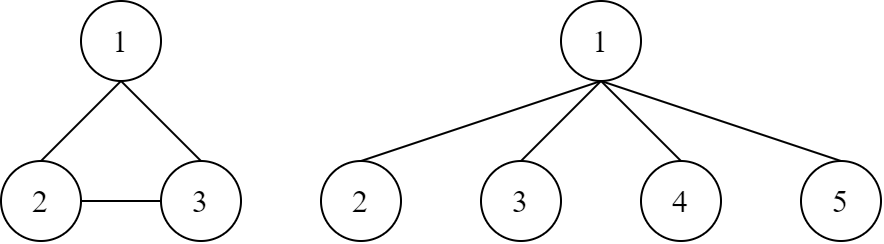
样例输入/输出 #1 的解析:
左图为该样例的输出。右图是该例子的另一个合理解。
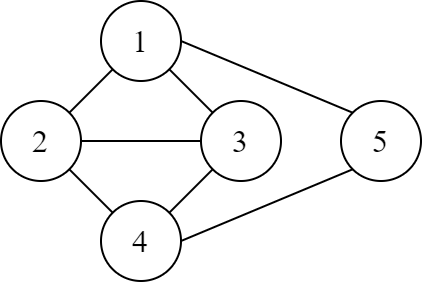
样例输入/输出 #3 的解析:
下图为该例的输出。
**本翻译由 AI 自动生成**
说明/提示
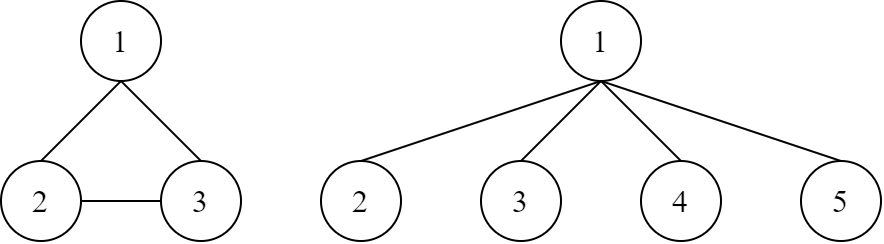
Explanation for the sample input/output #1
The graph on the left describes the output of this sample. The graph on the right describes another valid solution for this sample.
Explanation for the sample input/output #3
The following graph describes the output of this sample.
