CF2055F Cosmic Divide

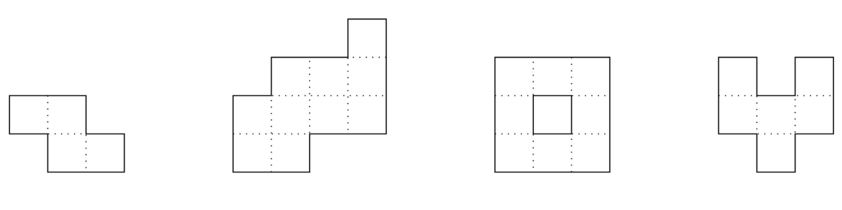
手握神器，现实的纤维向其真正的主人——Florida Man——屈服。 多连方（polyomino）是由一个或多个相等的 $1 \times 1$ 单元格通过边相连组成的连通图形。若对于多连方中任意两个在同一行或同一列的单元格，所有位于它们之间的单元格也都属于该多连方，则称其为凸多连方。下图展示了四个多连方，只有第一个和第二个是凸的。  你得到一个具有 $n$ 行且面积为偶数的凸多连方。对于每一行 $i$（$1 \le i \le n$），从第 $l_i$ 列到第 $r_i$ 列的单元格都属于该多连方。换句话说，第 $i$ 行包含 $r_i - l_i + 1$ 个属于多连方的单元格，分别为 $(i, l_i), (i, l_i + 1), \ldots, (i, r_i-1), (i, r_i)$。 如果两个多连方经过平移后可以完全重合，则称它们全等。注意，不允许旋转或翻转多连方。 请判断是否可以将给定的凸多连方划分为两个不相交且连通的多连方，并且这两个多连方全等。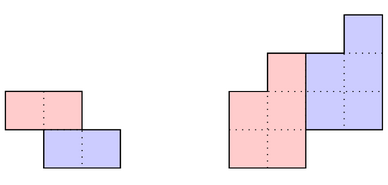下图展示了题目描述中前两个凸多连方的合法划分示例：  划分后得到的多连方不要求是凸的，并且每个单元格必须恰好属于其中一个划分出的多连方。 $^{\text{∗}}$ 若对于多连方中任意两个不同的单元格 $u \neq v$，存在一条由若干不同单元格 $s_1, s_2, \ldots, s_k$ 组成的路径，使得 $s_1 = u$，$s_k = v$，所有 $s_i$ 都属于该多连方，且对于每个 $1 \le i \le k-1$，$s_i$ 与 $s_{i+1}$ 共享一条边，则称该多连方是连通的。

每组测试数据包含多个测试用例。第一行包含一个整数 $t$（$1 \le t \le 10^4$），表示测试用例的数量。 每个测试用例的第一行包含一个整数 $n$（$1 \le n \le 2 \cdot 10^5$），表示多连方的行数。 接下来的 $n$ 行，每行包含两个整数 $l_i$ 和 $r_i$（$1 \le l_i \le r_i \le 10^9$），表示第 $i$ 行属于多连方的列区间。 保证多连方的面积为偶数，即 $\sum_{i=1}^n (r_i - l_i + 1) \equiv 0 \pmod{2}$。 保证所有测试用例中 $n$ 的总和不超过 $2 \cdot 10^5$。

对于每个测试用例，输出一行 "YES" 或 "NO"，表示是否可以按题目要求划分该多连方。 你可以以任意大小写输出答案，例如 "yEs"、"yes"、"Yes" 和 "YES" 都会被识别为肯定回答。

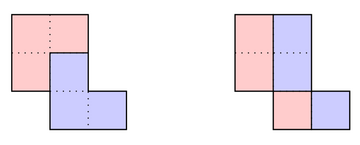
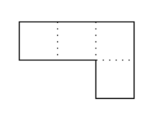
前两个测试用例对应题目描述中的多连方，并且可以如图所示进行划分。 第三个测试用例对应的多连方如下图所示，可以证明无法按要求划分。下图中的两种划分都不合法：  左侧的划分得到的多连方不是平移全等的，右侧的划分得到的多连方不是连通的。 第四个测试用例对应的多连方如下图所示，也无法按要求划分。  注意，虽然可以将其划分为两个 $1 \times 2$ 的矩形，但这两个矩形不是平移全等的。 由 ChatGPT 4.1 翻译