CF2056B Find the Permutation

You are given an undirected graph with $ n $ vertices, labeled from $ 1 $ to $ n $ . This graph encodes a hidden permutation $ ^{\text{∗}} $ $ p $ of size $ n $ . The graph is constructed as follows: - For every pair of integers $ 1 \le i < j \le n $ , an undirected edge is added between vertex $ p_i $ and vertex $ p_j $ if and only if $ p_i < p_j $ . Note that the edge is not added between vertices $ i $ and $ j $ , but between the vertices of their respective elements. Refer to the notes section for better understanding. Your task is to reconstruct and output the permutation $ p $ . It can be proven that permutation $ p $ can be uniquely determined. $ ^{\text{∗}} $ A permutation of length $ n $ is an array consisting of $ n $ distinct integers from $ 1 $ to $ n $ in arbitrary order. For example, $ [2,3,1,5,4] $ is a permutation, but $ [1,2,2] $ is not a permutation ( $ 2 $ appears twice in the array), and $ [1,3,4] $ is also not a permutation ( $ n=3 $ but there is $ 4 $ in the array).

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 500 $ ). The description of the test cases follows. The first line of each test case contains a single integer $ n $ ( $ 1 \le n \le 1000 $ ). The $ i $ -th of the next $ n $ lines contains a string of $ n $ characters $ g_{i, 1}g_{i, 2}\ldots g_{i, n} $ ( $ g_{i, j} = \mathtt{0} $ or $ g_{i, j} = \mathtt{1} $ ) — the adjacency matrix. $ g_{i, j} = \mathtt{1} $ if and only if there is an edge between vertex $ i $ and vertex $ j $ . It is guaranteed that there exists a permutation $ p $ which generates the given graph. It is also guaranteed that the graph is undirected and has no self-loops, meaning $ g_{i, j} = g_{j, i} $ and $ g_{i, i} = \mathtt{0} $ . It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 1000 $ .

For each test case, output $ n $ integers $ p_1, p_2, \ldots, p_n $ representing the reconstructed permutation.

In the first case $ p = [1] $ . Since there are no pairs $ 1 \le i < j \le n $ , there are no edges in the graph. The graph in the second case is shown below. For example, when we choose $ i = 3 $ and $ j = 4 $ , we add an edge between vertices $ p_i = 1 $ and $ p_j = 3 $ , because $ p_i < p_j $ . However, when we choose $ i = 2 $ and $ j = 3 $ , $ p_i = 2 $ and $ p_j = 1 $ , so $ p_i < p_j $ doesn't hold. Therefore, we don't add an edge between $ 2 $ and $ 1 $ .  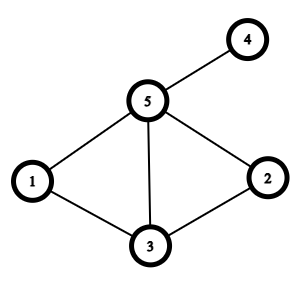In the third case, there are no edges in the graph, so there are no pairs of integers $ 1 \le i < j \le n $ such that $ p_i < p_j $ . Therefore, $ p = [6, 5, 4, 3, 2, 1] $ .