CF2056B Find the Permutation

给定一个有 $n$ 个顶点的无向图，顶点标记为从 $1$ 到 $n$ 。此图编码了一个长度为 $n$ 的隐藏排列 $^{\text{∗}}$ $p$ 。该图的构建方式如下： - 对于每一对满足 $1 \le i < j \le n$ 的整数，当且仅当 $p_i < p_j$ 时，在顶点 $p_i$ 和顶点 $p_j$ 之间添加一条无向边。请注意，边不是添加在顶点 $i$ 和顶点 $j$ 之间，而是添加在它们对应元素的顶点之间。参考注释部分可获得更好的理解。 你的任务是重构并输出排列 $p$ 。可以证明排列 $p$ 是唯一确定的。 > 长度为 $n$ 的排列是一个由 $n$ 个从 $1$ 到 $n$ 的不同整数按任意顺序组成的数组。例如，$[2,3,1,5,4]$ 是一个排列，但 $[1,2,2]$ 不是排列（数组中 $2$ 出现了两次），$[1,3,4]$ 也不是排列（$n = 3$ 但数组中有 $4$ ）。

每个测试包含多个测试用例。第一行包含测试用例的数量 $t$ （$1 \le t \le 500$）。接下来是测试用例的描述。 每个测试用例的第一行包含一个整数 $n$ （$1 \le n \le 1000$）。 接下来 $n$ 行的第 $i$ 行包含一个由 $n$ 个字符 $g_{i, 1}g_{i, 2}\ldots g_{i, n}$ 组成的字符串（$g_{i, j} = \mathtt{0}$ 或 $g_{i, j} = \mathtt{1}$）—— 邻接矩阵。当且仅当顶点 $i$ 和顶点 $j$ 之间有一条边时，$g_{i, j} = \mathtt{1}$ 。 保证存在一个排列 $p$ 生成给定的图。同时保证图是无向的且没有自环，即 $g_{i, j} = g_{j, i}$ 且 $g_{i, i} = \mathtt{0}$ 。 保证所有测试用例中 $n$ 的总和不超过 $1000$ 。

对于每个测试用例，输出 $n$ 个整数 $p_1, p_2, \ldots, p_n$ 表示重构的排列。

In the first case $ p = [1] $ . Since there are no pairs $ 1 \le i < j \le n $ , there are no edges in the graph. The graph in the second case is shown below. For example, when we choose $ i = 3 $ and $ j = 4 $ , we add an edge between vertices $ p_i = 1 $ and $ p_j = 3 $ , because $ p_i < p_j $ . However, when we choose $ i = 2 $ and $ j = 3 $ , $ p_i = 2 $ and $ p_j = 1 $ , so $ p_i < p_j $ doesn't hold. Therefore, we don't add an edge between $ 2 $ and $ 1 $ .  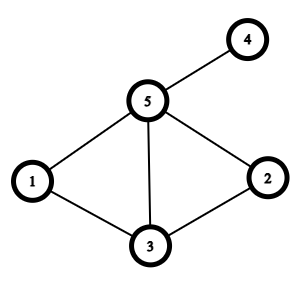In the third case, there are no edges in the graph, so there are no pairs of integers $ 1 \le i < j \le n $ such that $ p_i < p_j $ . Therefore, $ p = [6, 5, 4, 3, 2, 1] $ .