CF2057G Secret Message

每个周六晚上，平行班的老师亚历山大 B，总会把一封密码信息写在交互式在线白板上，发送给另一位老师亚历山大 G。这封信相当重要，而亚历山大 G 正在授课，因此在线白板就成了一个理想的秘密传递工具。 这个白板是一个由 $n$ 行 $m$ 列构成的网格。网格中每个单元格大小是 $1 \times 1$。部分单元格已经填满，用符号 "." 表示，不能在其中书写；剩下的未填满的单元格称为自由单元格，用符号 "#" 代表。 我们需要关注白板的两个特性： - $s$：自由单元格的数量。 - $p$：由这些自由单元格构成的图形的边界周长。 设 $A$ 为当前所有自由单元格的集合。你的任务是从中找到一个子集 $S \subseteq A$，满足以下条件： - $|S| \le \frac{1}{5} \cdot (s+p)$，即集合 $S$ 的大小不超过 $s$ 和 $p$ 的加和的五分之一。 - 每一个自由单元格，要么已经在 $S$ 中，要么与 $S$ 中的某个单元格相邻（共用一条边）。 可以证明，总有这样的集合 $S$ 存在，你只需找到任意符合条件的一个即可。

首先输入一个整数 $t$ 表示测试用例的数量（$1 \le t \le 80\,000$）。 每个测试用例的第一行包含两个整数 $n$ 和 $m$ （$1 \le n, m \le 2 \cdot 10^6$），分别表示网格的行数和列数。 接下来的 $n$ 行给出网格的具体描述。 所有测试用例中，所有 $n \cdot m$ 的总和不超过 $2 \cdot 10^6$。

对于每个测试用例，输出 $n$ 行，每行有 $m$ 个字符，表示网格中的单元状态： - "#" 表示该单元格在 $A$ 中但不在 $S$ 中； - "S" 表示该单元格同时在 $A$ 和 $S$ 中； - "." 表示该单元格既不在 $A$ 中也不在 $S$ 中。

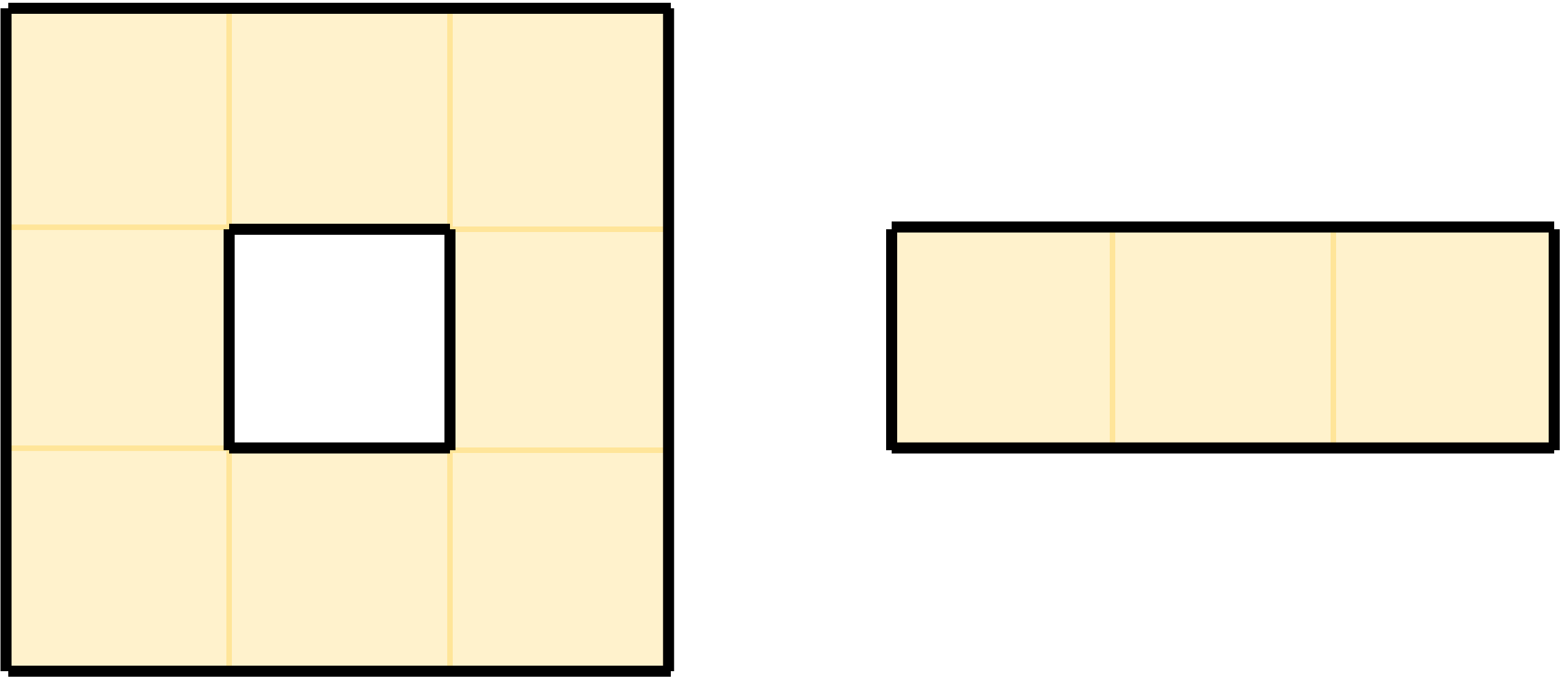
例如： - 在第一个例子中，$s=5$ 和 $p=12$，所以 $S$ 的单元格数量不能超过 $\frac{1}{5} \cdot (5+12) = 3.4$，即 $|S| \le 3$。给出的 $S$ 集合包含 1 个单元格，符合条件。 - 在第二个例子中，$s=12$ 和 $p=16$，所以 $S$ 的单元格数量不能超过 $\frac{1}{5} \cdot (12+16)= 5.6$，即 $|S| \le 5$。给出的 $S$ 集合包含 4 个单元格，符合条件。 - 在第三个例子中说明了周长的概念。任何网格图形都有一个由线段组成的边界，边界线段的长度总和即为周长。在示例中，黑色粗线标示的是自由单元格形成图形的边界，其总长度为 $p=24$。同时，$s=11$，故上限为 $|S| \le 7$，给出的 $S$ 集合大小为 6，符合条件。  **本翻译由 AI 自动生成**