CF2062D Balanced Tree
题目描述
给定一棵包含 $n$ 个节点的树 $^{\text{∗}}$,每个节点 $i$ 有取值范围 $[l_i, r_i]$。你可以为第 $i$ 个节点选择一个初始值 $a_i$ 满足 $l_i \le a_i \le r_i$。当所有节点值相等时,该树称为平衡树,其值定义为任意节点的值。
每次操作中,你可以选择两个节点 $u$ 和 $v$,在以 $u$ 为根的整棵树结构下,将节点 $v$ 的子树 $^{\text{†}}$ 中所有节点的值增加 $1$。注意 $u$ 可以与 $v$ 相同。
你的目标是通过若干次操作使树变为平衡状态。求操作完成后树的最小可能值(无需最小化操作次数)。
$^{\text{∗}}$ 树是一个无环的连通图。
$^{\text{†}}$ 在以 $u$ 为根时,若从根 $u$ 到节点 $w$ 的所有路径都必须经过节点 $v$,则称 $w$ 属于 $v$ 的子树。
输入格式
第一行输入包含一个整数 $t$($1 \leq t \leq 10^5$)——测试用例数量。
每个测试用例:
- 第一行包含一个整数 $n$($1 \le n \le 2 \cdot 10^5$)——树的节点数。
- 接下来 $n$ 行,第 $i$ 行包含两个整数 $l_i, r_i$($0 \le l_i \le r_i \le 10^9$)——第 $i$ 个节点的取值范围。
- 接下来 $n-1$ 行描述树的边。第 $i$ 行包含两个整数 $u_i, v_i$($1 \le u_i, v_i \le n$,$u_i \neq v_i$)——连接 $u_i$ 和 $v_i$ 的边。保证输入构成一棵树。
保证所有测试用例的 $n$ 之和不超过 $2 \cdot 10^5$。
输出格式
对于每个测试用例,输出一个整数——操作完成后所有 $a_i$ 可达到的相等值的最小可能值。可以证明答案总是存在。
说明/提示
第一个测试用例中,可以选择 $a = [6, 6, 0, 5]$。
通过以下操作使所有 $a_i$ 相等:
1. 选择 $u=4$,$v=3$,执行该操作 $5$ 次。
2. 选择 $u=1$,$v=3$,执行该操作 $6$ 次。
完整过程如下(括号内数字为 $a$ 的元素):
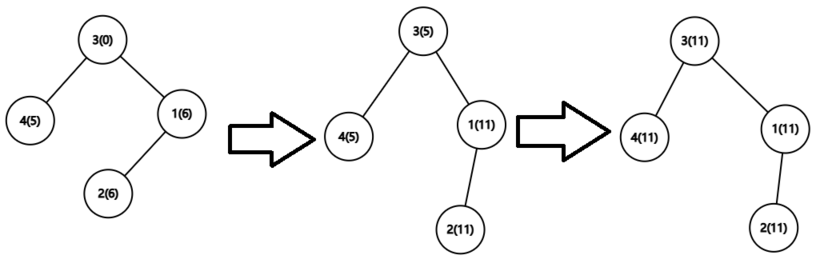
可以证明这是最优解。
翻译由 DeepSeek R1 完成