CF2064E Mycraft Sand Sort

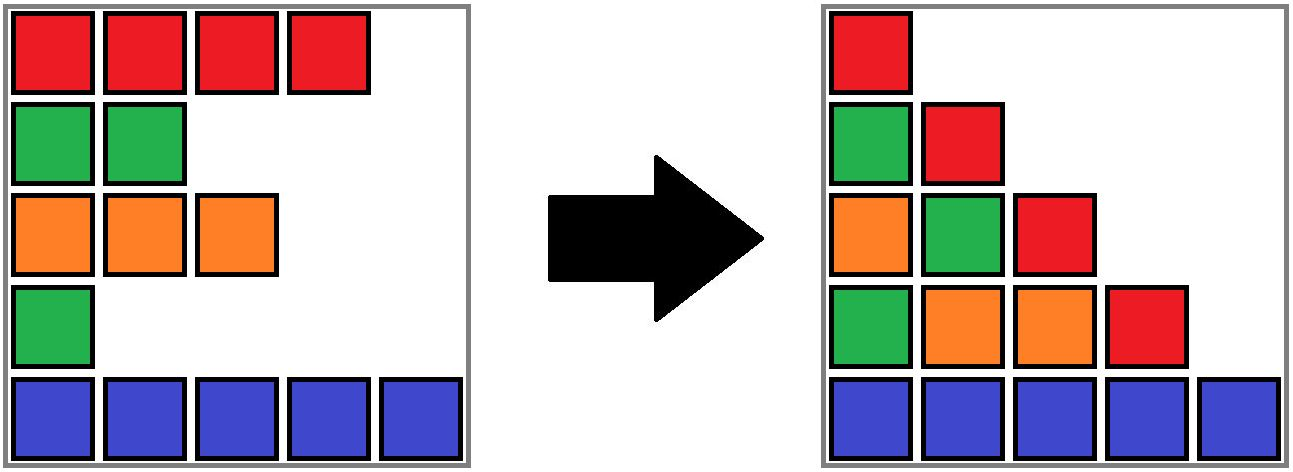
Steve 有一个排列 $p$ 和一个数组 $c$，它们的长度均为 $n$。Steve 希望对排列 $p$ 进行排序。 Steve 有无限多的彩色沙块，他用这些沙块发明了一种基于物理的排序方法，称为重力排序。具体来说，对 $p$ 进行重力排序的步骤如下： - 对于所有满足 $1 \le i \le n$ 的 $i$，在所有 $1 \le j \le p_i$ 的位置 $(i, j)$ 上放置一个颜色为 $c_i$ 的沙块。这里，位置 $(x, y)$ 表示从上往下第 $x$ 行、从左往右第 $y$ 列的格子。 - 对整个数组施加向下的重力，使所有沙块尽可能下落。  这是第三个测试用例的重力排序示例。$p = [4, 2, 3, 1, 5]$，$c = [2, 1, 4, 1, 5]$。 Alex 在 Steve 完成重力排序后观察沙块，想知道有多少对数组 $(p', c')$，其中 $p'$ 是一个排列，能够产生与当前相同的沙块布局。注意，原始的数组对 $(p, c)$ 总是会被计入答案。 请你帮 Alex 计算这个数量。由于答案可能很大，请对 $998\,244\,353$ 取模后输出。 $^{\text{∗}}$ 长度为 $n$ 的排列是一个包含 $1$ 到 $n$ 的 $n$ 个互不相同整数的数组。例如，$[2,3,1,5,4]$ 是一个排列，但 $[1,2,2]$ 不是（$2$ 出现了两次），$[1,3,4]$ 也不是（$n=3$，但出现了 $4$）。

第一行包含一个整数 $t$（$1 \le t \le 10^4$）——表示测试用例的数量。 每个测试用例的第一行包含一个整数 $n$（$1 \le n \le 2 \cdot 10^5$）——数组的长度。 接下来一行包含 $n$ 个互不相同的整数 $p_1,p_2,\ldots,p_n$（$1 \le p_i \le n$）——排列 $p$ 的元素。 接下来一行包含 $n$ 个整数 $c_1,c_2,\ldots,c_n$（$1 \le c_i \le n$）——数组 $c$ 的元素。 所有测试用例中 $n$ 的总和不超过 $2 \cdot 10^5$。

对于每个测试用例，输出一个整数，表示 Steve 可能开始的数组对 $(p', c')$ 的数量，对 $998\,244\,353$ 取模。

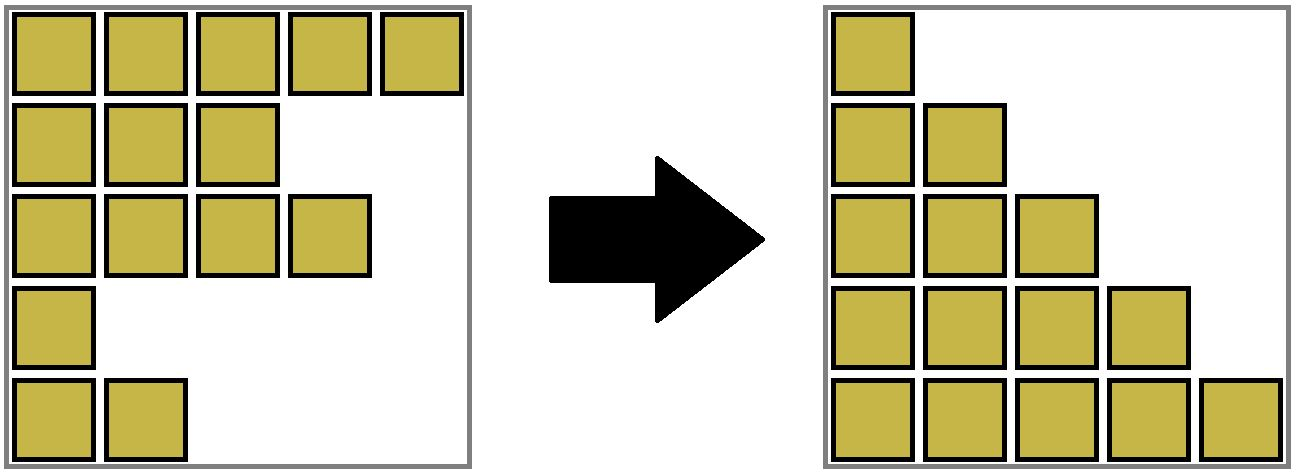
第二个测试用例如下图所示。  这是第二个测试用例的重力排序结果。可以证明，$p$ 的所有排列都会产生相同的结果，并且 $c$ 必须为 $[1,1,1,1,1]$（因为所有沙块颜色必须相同），所以答案是 $5! = 120$。 第三个测试用例如题面所示。可以证明，没有其他数组 $p$ 和 $c$ 能产生相同的最终结果，所以答案是 $1$。 由 ChatGPT 4.1 翻译