CF2064E Mycraft Sand Sort

Steve has a permutation $ ^{\text{∗}} $ $ p $ and an array $ c $ , both of length $ n $ . Steve wishes to sort the permutation $ p $ . Steve has an infinite supply of coloured sand blocks, and using them he discovered a physics-based way to sort an array of numbers called gravity sort. Namely, to perform gravity sort on $ p $ , Steve will do the following: - For all $ i $ such that $ 1 \le i \le n $ , place a sand block of color $ c_i $ in position $ (i, j) $ for all $ j $ where $ 1 \le j \le p_i $ . Here, position $ (x, y) $ denotes a cell in the $ x $ -th row from the top and $ y $ -th column from the left. - Apply downwards gravity to the array, so that all sand blocks fall as long as they can fall. 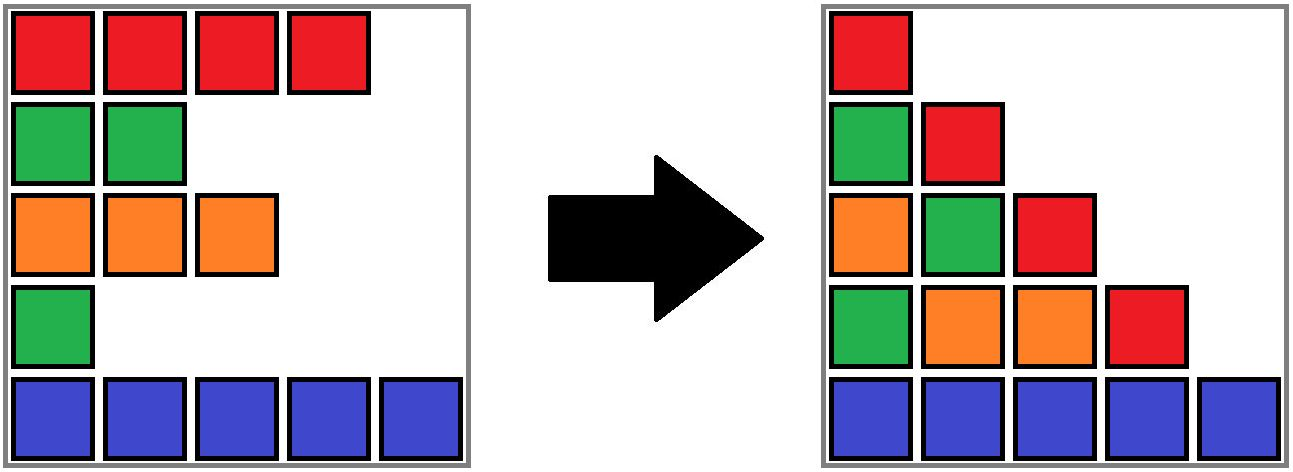 An example of gravity sort for the third testcase. $ p = [4, 2, 3, 1, 5] $ , $ c = [2, 1, 4, 1, 5] $ Alex looks at Steve's sand blocks after performing gravity sort and wonders how many pairs of arrays $ (p',c') $ where $ p' $ is a permutation would have resulted in the same layout of sand. Note that the original pair of arrays $ (p, c) $ will always be counted. Please calculate this for Alex. As this number could be large, output it modulo $ 998\,244\,353 $ . $ ^{\text{∗}} $ A permutation of length $ n $ is an array consisting of $ n $ distinct integers from $ 1 $ to $ n $ in arbitrary order. For example, $ [2,3,1,5,4] $ is a permutation, but $ [1,2,2] $ is not a permutation ( $ 2 $ appears twice in the array), and $ [1,3,4] $ is also not a permutation ( $ n=3 $ but there is a $ 4 $ in the array).

The first line contains an integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases. The first line of each testcase contains an integer $ n $ ( $ 1 \le n \le 2 \cdot 10^5 $ ) — the lengths of the arrays. The second line of each testcase contains $ n $ distinct integers $ p_1,p_2,\ldots,p_n $ ( $ 1 \le p_i \le n $ ) — the elements of $ p $ . The following line contains $ n $ integers $ c_1,c_2,\ldots,c_n $ ( $ 1 \le c_i \le n $ ) — the elements of $ c $ . The sum of $ n $ across all testcases does not exceed $ 2 \cdot 10^5 $ .

For each testcase, output the number of pairs of arrays $ (p', c') $ Steve could have started with, modulo $ 998\,244\,353 $ .

The second test case is shown below. 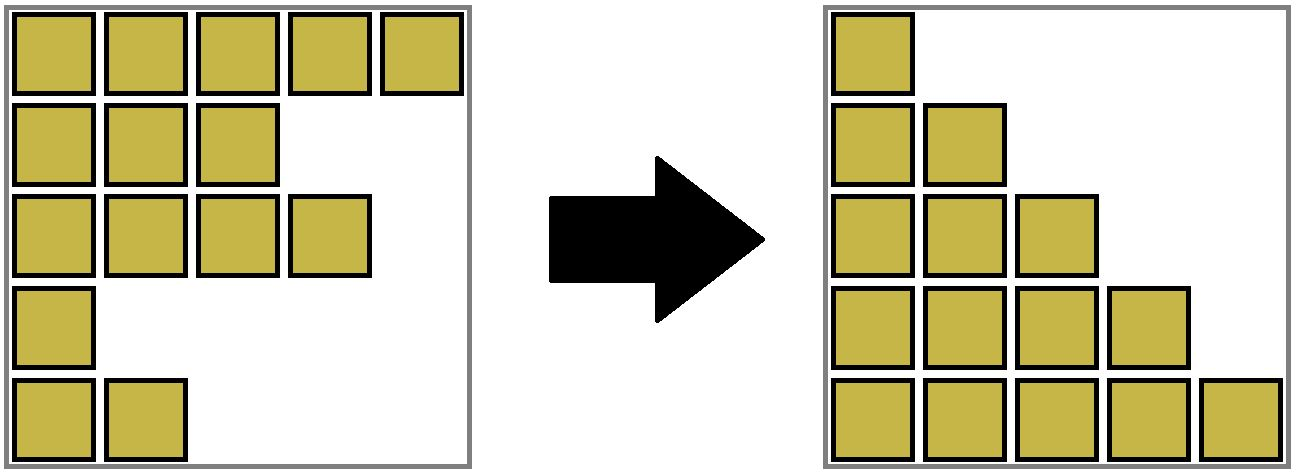 Gravity sort of the second testcase.It can be shown that permutations of $ p $ will yield the same result, and that $ c $ must equal $ [1,1,1,1,1] $ (since all sand must be the same color), so the answer is $ 5! = 120 $ . The third test case is shown in the statement above. It can be proven that no other arrays $ p $ and $ c $ will produce the same final result, so the answer is $ 1 $ .