CF2068E Porto Vs. Benfica

FC Porto 和 SL Benfica 是葡萄牙最大的两个足球俱乐部。当两队比赛时，大量球迷会从全国各地前往观赛，其中包括计划从里斯本前往波尔图的 Benfica 球迷俱乐部。为避免与 Porto 球迷俱乐部发生冲突，警方希望尽可能延迟他们的到达时间。 葡萄牙的公路网可建模为一个简单、无向、无权、连通的图，包含 $n$ 个顶点和 $m$ 条边。顶点代表城镇，边代表道路。顶点 $1$ 对应里斯本（球迷的起点），顶点 $n$ 对应波尔图（球迷的目的地）。球迷俱乐部希望最小化前往波尔图所经过的道路数量。 警方始终密切追踪球迷的位置。为延迟其到达，警方可在任意时刻封锁一条道路（前提是球迷当前不在该道路上通行）。此操作只能执行一次，且被封锁的道路将永久不可用。封锁后，球迷会立即得知该信息并调整路线。同时球迷知晓警方会封锁某条道路，并据此规划路线。 假设双方均采取最优策略，求球迷从里斯本到波尔图所需经过的最少道路数量。若警方能永久阻止球迷到达波尔图，则输出 $-1$。

第一行包含两个整数 $n$ 和 $m$（$2 \leq n \leq 200\,000$，$n - 1 \leq m \leq \min\{n(n - 1)/2, 200\,000\}$）——城镇数量和道路数量。 接下来 $m$ 行每行包含两个整数 $s_i$ 和 $t_i$（$1 \leq s_i, t_i \leq n$）——表示第 $i$ 条道路连接的两个城镇。 保证公路网连通，每条道路连接两个不同城镇，且无重复道路。

输出球迷俱乐部从里斯本到波尔图所需经过的最少道路数量。

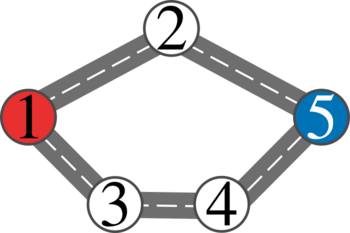
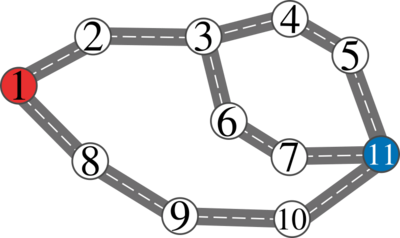
第一个样例的公路网结构如下：  警方最优策略是等待球迷到达与目的地相邻的顶点（如顶点 $5$）后封锁该顶点到目的地的边。球迷最优策略是先沿上方路径（$1 \rightarrow 2$），在发现 $2$ 到 $5$ 的边被封锁后，返回 $2 \rightarrow 1$ 并沿下方路径（$1 \rightarrow 3 \rightarrow 4 \rightarrow 5$）。此时经过的道路总数为 $5$。 第二个样例的公路网结构如下：  存在多种策略，但最优方案为：球迷沿上方路径（$1 \rightarrow 2 \rightarrow 3 \rightarrow 4 \rightarrow 5$），警方封锁边 $5 \rightarrow 11$，球迷绕行 $5 \rightarrow 4 \rightarrow 3 \rightarrow 6 \rightarrow 7 \rightarrow 11$。总经过道路数为 $9$。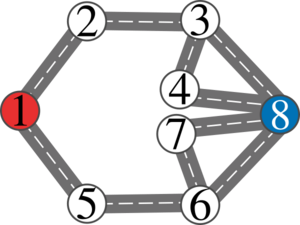 第三个样例的公路网结构如下：  警方最优策略为：若球迷到达顶点 $2$ 则封锁边 $2 \rightarrow 3$，若到达顶点 $5$ 则封锁边 $5 \rightarrow 6$。球迷最优路径为 $1 \rightarrow 2 \rightarrow 1 \rightarrow 5 \rightarrow 6 \rightarrow 8$，总经过道路数为 $5$。 翻译由 DeepSeek R1 完成