CF2068H Statues

某市市长计划在城市交叉路口放置 $n$ 座雕像。城市交叉路口的坐标为所有整数坐标点 $(x, y)$。交叉路口之间的距离使用曼哈顿距离计算，定义如下： $$ \text{distance}((x_1, y_1), (x_2, y_2)) = |x_1 - x_2| + |y_1 - y_2|. $$ 市议会对雕像的放置提出了以下要求： - 第一座雕像必须放置在 $(0, 0)$； - 第 $n$ 座雕像必须放置在 $(a, b)$； - 对于 $i = 1, \dots, n-1$，第 $i$ 座雕像与第 $(i+1)$ 座雕像之间的距离必须为 $d_i$。允许将多座雕像放置在同一个交叉路口。 请帮助市长找到满足条件的 $n$ 座雕像的放置方案，或判定其不存在。

第一行包含一个整数 $n$（$3 \le n \le 50$）——雕像的数量。 第二行包含两个整数 $a$ 和 $b$（$0 \le a, b \le 10^9$）——第 $n$ 座雕像必须放置的坐标。 第三行包含 $n-1$ 个整数 $d_1, \dots, d_{n-1}$（$0 \le d_i \le 10^9$）——第 $i$ 座与第 $(i+1)$ 座雕像之间的距离。

若存在有效放置方案，输出 $\texttt{YES}$，否则输出 $\texttt{NO}$。 若存在有效方案，在接下来的 $n$ 行中输出具体方案。第 $i$ 行包含两个整数 $x_i$ 和 $y_i$，表示第 $i$ 座雕像的坐标。若有多个解，输出任意一个即可。

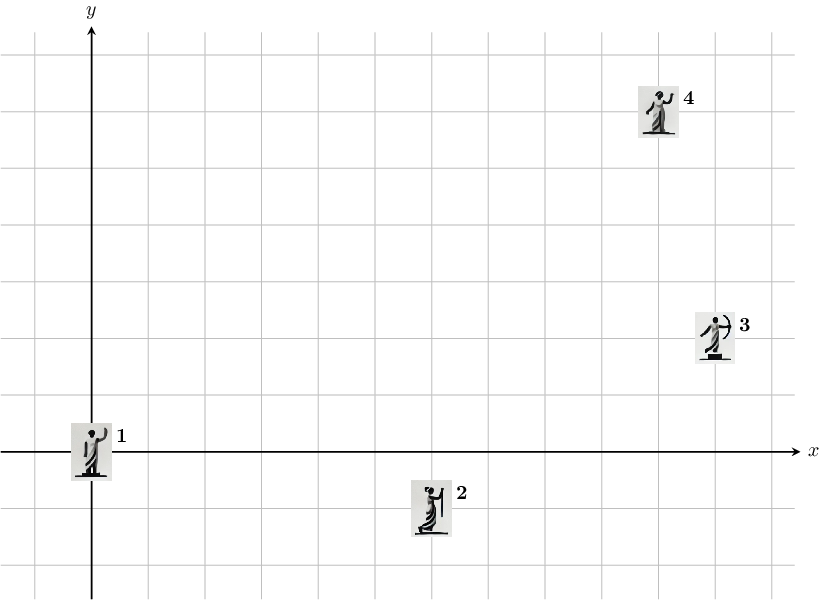
第一个样例中，不存在满足条件的 3 座雕像的放置方案。 第二个样例中，图示展示了一种可能的有效方案（注意并非唯一解）：  翻译由 DeepSeek R1 完成