CF2068H Statues

The mayor of a city wants to place $n$ statues at intersections around the city. The intersections in the city are at all points $(x, y)$ with integer coordinates. Distances between intersections are measured using Manhattan distance, defined as follows: $$ \text{distance}((x_1, y_1), (x_2, y_2)) = |x_1 - x_2| + |y_1 - y_2|. $$ The city council has provided the following requirements for the placement of the statues: - The first statue is placed at $(0, 0)$; - The $n$\-th statue is placed at $(a, b)$; - For $i = 1, \dots, n-1$, the distance between the $i$\-th statue and the $(i+1)$\-th statue is $d_i$. It is allowed to place multiple statues at the same intersection. Help the mayor find a valid arrangement of the $n$ statues, or determine that it does not exist.

The first line contains an integer $ n $ ( $ 3 \le n \le 50 $ ) — the number of statues. The second line contains two integers $ a $ and $ b $ ( $ 0 \le a, b \le 10^9 $ ) — the coordinates of the intersection where the $ n $ -th statue must be placed. The third line contains $ n-1 $ integers $ d_1, \dots, d_{n-1} $ ( $ 0 \le d_i \le 10^9 $ ) — the distance between the $ i $ -th statue and the $ (i+1) $ -th statue.

Print $ \texttt{YES} $ if there is a valid arrangement of the $ n $ statues. Otherwise, print $ \texttt{NO} $ . If there is a valid arrangement, print a valid arrangement in the following $ n $ lines. The $ i $ -th of these lines must contain two integers $ x_i $ and $ y_i $ — the coordinates of the intersection where the $ i $ -th statue is placed. You can print any valid arrangement if multiple exist.

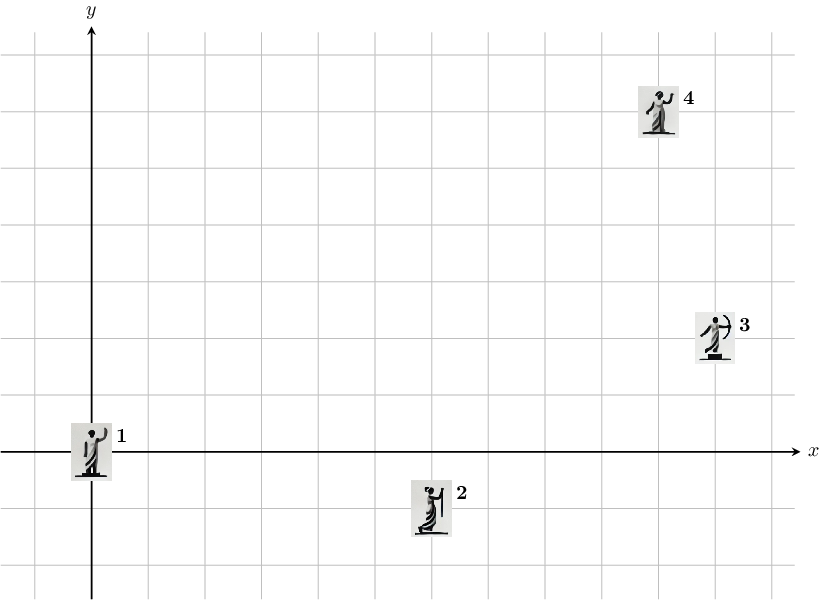
In the first sample, there is no valid arrangement of the 3 statues. In the second sample, the sample output is shown in the following picture. Note that this is not the only valid arrangement of the 4 statues.