CF2069F Graph Inclusion

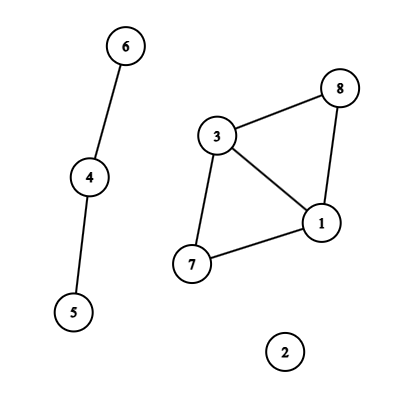
在无向图中，连通分量（connected component）定义为满足以下条件的顶点集合 $S$： - 对于 $S$ 中的任意顶点对 $(u, v)$，存在从 $u$ 到 $v$ 的路径； - 不存在属于 $S$ 外部的顶点与 $S$ 内部的顶点之间存在路径。 例如，下图中的图有三个连通分量：$\{1, 3, 7, 8\}$、$\{2\}$、$\{4, 5, 6\}$。  我们称图 $A$ 包含（include）图 $B$，当且仅当图 $B$ 的每个连通分量都是图 $A$ 某个连通分量的子集。 给定两个图 $A$ 和 $B$，它们均包含 $n$ 个顶点（编号为 $1$ 到 $n$）。初始时两个图都没有边。你需要处理以下两种类型的查询： - 向其中一个图添加一条边； - 从其中一个图中删除一条边。 在每次查询后，你需要计算为了使图 $A$ 包含图 $B$ 所需要向图 $A$ 添加的最小边数，并输出该数值。注意这些边不会被实际添加，仅需计算数量。

第一行包含两个整数 $n$ 和 $q$（$2 \le n \le 4 \cdot 10^5$；$1 \le q \le 4 \cdot 10^5$）——分别表示顶点数和查询数。 接下来 $q$ 行描述查询，其中第 $i$ 行描述第 $i$ 个查询。查询描述以一个字符 $c_i$（A 或 B）开头，表示该查询作用的图。接着是两个整数 $x_i$ 和 $y_i$（$1 \le x_i, y_i \le n$；$x_i \ne y_i$）。如果对应图中存在边 $(x_i, y_i)$，则删除该边；否则添加该边。

对于每个查询，输出一个整数——为使图 $A$ 包含图 $B$ 所需向图 $A$ 添加的最小边数。 翻译由 DeepSeek R1 完成