CF2069F Graph Inclusion

A connected component of an undirected graph is defined as a set of vertices $ S $ of this graph such that: - for every pair of vertices $ (u, v) $ in $ S $ , there exists a path between vertices $ u $ and $ v $ ; - there is no vertex outside $ S $ that has a path to a vertex within $ S $ . For example, the graph in the picture below has three components: $ \{1, 3, 7, 8\} $ , $ \{2\} $ , $ \{4, 5, 6\} $ . 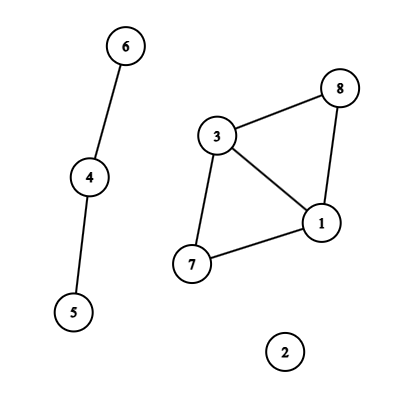We say that graph $ A $ includes graph $ B $ if every component of graph $ B $ is a subset of some component of graph $ A $ . You are given two graphs, $ A $ and $ B $ , both consisting of $ n $ vertices numbered from $ 1 $ to $ n $ . Initially, there are no edges in the graphs. You must process queries of two types: - add an edge to one of the graphs; - remove an edge from one of the graphs. After each query, you have to calculate the minimum number of edges that have to be added to $ A $ so that $ A $ includes $ B $ , and print it. Note that you don't actually add these edges, you just calculate their number.

The first line contains two integers $ n $ and $ q $ ( $ 2 \le n \le 4 \cdot 10^5 $ ; $ 1 \le q \le 4 \cdot 10^5 $ ) — the number of vertices and queries, respectively. Next, there are $ q $ lines, where the $ i $ -th line describes the $ i $ -th query. The description of the query begins with the character $ c_i $ (either A or B) — the graph to which the query should be applied. Then, two integers $ x_i $ and $ y_i $ follow ( $ 1 \le x_i, y_i \le n $ ; $ x_i \ne y_i $ ). If there is an edge $ (x_i, y_i) $ in the corresponding graph, it should be removed; otherwise, it should be added to that graph.

For each query, print one integer — the minimum number of edges that you have to add to the graph $ A $ so that it includes $ B $ .