CF2071E LeaFall

给定一棵包含 $n$ 个顶点的树 $^{\text{∗}}$。每个顶点 $i$（$1 \le i \le n$）会以 $\frac{p_i}{q_i}$ 的概率掉落。求最终形成的森林 $^{\text{‡}}$ 中不同顶点构成叶子节点 $^{\text{§}}$ 的无序对 $^{\text{†}}$ 数量的期望值，结果对 $998\,244\,353$ 取模。 注意：当顶点 $v$ 掉落时，其自身及所有相连的边将被移除，但相邻顶点的掉落状态不受 $v$ 的影响。 $^{\text{∗}}$ 树是一个无环的连通图。 $^{\text{†}}$ 无序对指不考虑元素顺序的二元组。例如，无序对 $(1, 2)$ 与 $(2, 1)$ 视为相同。 $^{\text{‡}}$ 叶子节点指恰好连接一条边的顶点。 $^{\text{§}}$ 森林是多个不连通树的集合。

每个测试包含多个测试用例。第一行包含测试用例数量 $t$（$1 \le t \le 10^4$）。接下来是各个测试用例的描述。 每个测试用例的第一行包含一个整数 $n$（$1 \le n \le 10^5$）。 接下来的 $n$ 行中，第 $i$ 行包含两个整数 $p_i$ 和 $q_i$（$1 \le p_i < q_i < 998\,244\,353$）。 接下来的 $n - 1$ 行每行包含两个整数 $u$ 和 $v$（$1 \le u, v \le n$，$u \neq v$）——表示通过边连接的顶点编号。 保证输入的边构成一棵树。 保证所有测试用例的 $n$ 之和不超过 $10^5$。

对于每个测试用例，输出一个整数——满足条件的无序对数量的期望值模 $998\,244\,353$ 的结果。 形式化地，设 $M = 998\,244\,353$。可以证明精确答案可表示为最简分数 $\frac{p}{q}$，其中 $q \not \equiv 0 \pmod{M}$。输出 $p \cdot q^{-1} \bmod M$。即输出满足 $0 \le x < M$ 且 $x \cdot q \equiv p \pmod{M}$ 的整数 $x$。

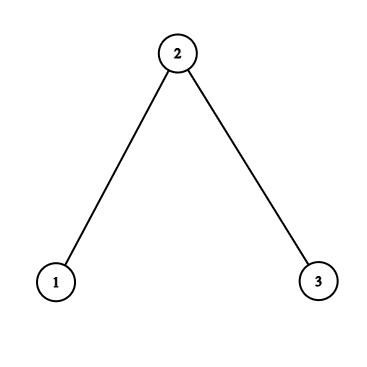
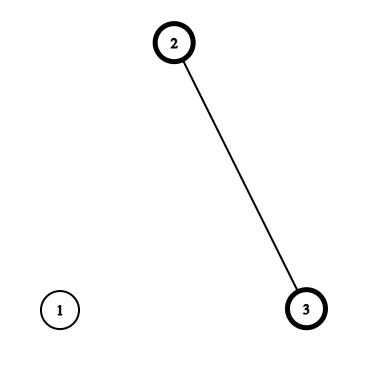
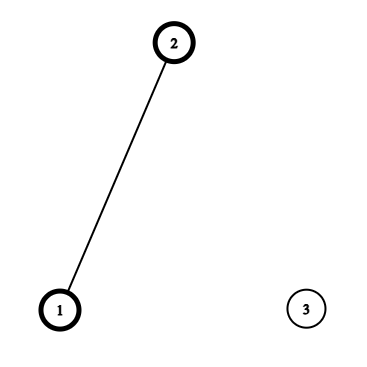
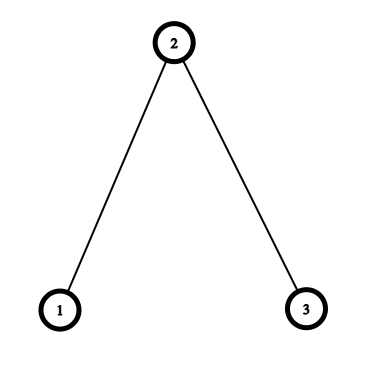
第一个测试用例中，树仅有一个顶点（非叶子节点），因此答案为 $0$。 第二个测试用例的树结构如下图所示：  未掉落的顶点以粗体表示。考虑以下三种情况：  该情况出现概率为 $\left( \frac{1}{2} \right)^3$，唯一满足条件的无序对是 $(2, 3)$。  该情况出现概率为 $\left( \frac{1}{2} \right)^3$，唯一满足条件的无序对是 $(2, 1)$。  该情况出现概率为 $\left( \frac{1}{2} \right)^3$，唯一满足条件的无序对是 $(1, 3)$。 其他情况中不存在满足条件的无序对。因此答案为 $\frac{1 + 1 + 1}{8} = \frac{3}{8}$，模 $998\,244\,353$ 的结果为 $623\,902\,721$。 翻译由 DeepSeek R1 完成