CF2071E LeaFall

You are given a tree $ ^{\text{∗}} $ with $ n $ vertices. Over time, each vertex $ i $ ( $ 1 \le i \le n $ ) has a probability of $ \frac{p_i}{q_i} $ of falling. Determine the expected value of the number of unordered pairs $ ^{\text{†}} $ of distinct vertices that become leaves $ ^{\text{‡}} $ in the resulting forest $ ^{\text{§}} $ , modulo $ 998\,244\,353 $ . Note that when vertex $ v $ falls, it is removed along with all edges connected to it. However, adjacent vertices remain unaffected by the fall of $ v $ . $ ^{\text{∗}} $ A tree is a connected graph without cycles. $ ^{\text{†}} $ An unordered pair is a collection of two elements where the order in which the elements appear does not matter. For example, the unordered pair $ (1, 2) $ is considered the same as $ (2, 1) $ . $ ^{\text{‡}} $ A leaf is a vertex that is connected to exactly one edge. $ ^{\text{§}} $ A forest is a graph without cycles

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 10^4 $ ). The description of the test cases follows. The first line of each test case contains a single integer $ n $ ( $ 1 \le n \le 10^5 $ ). The $ i $ -th line of the following $ n $ lines contains two integers $ p_i $ and $ q_i $ ( $ 1 \le p_i < q_i < 998\,244\,353 $ ). Each of the following $ n - 1 $ lines contains two integers $ u $ and $ v $ ( $ 1 \le u, v \le n $ , $ u \neq v $ ) — the indices of the vertices connected by an edge. It is guaranteed that the given edges form a tree. It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 10^5 $ .

For each test case, output a single integer — the expected value of the number of unordered pairs of distinct vertices that become leaves in the resulting forest modulo $ 998\,244\,353 $ . Formally, let $ M = 998\,244\,353 $ . It can be shown that the exact answer can be expressed as an irreducible fraction $ \frac{p}{q} $ , where $ p $ and $ q $ are integers and $ q \not \equiv 0 \pmod{M} $ . Output the integer equal to $ p \cdot q^{-1} \bmod M $ . In other words, output such an integer $ x $ that $ 0 \le x < M $ and $ x \cdot q \equiv p \pmod{M} $ .

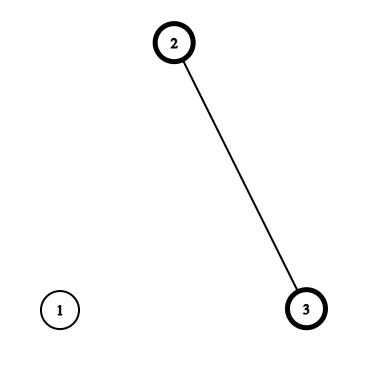
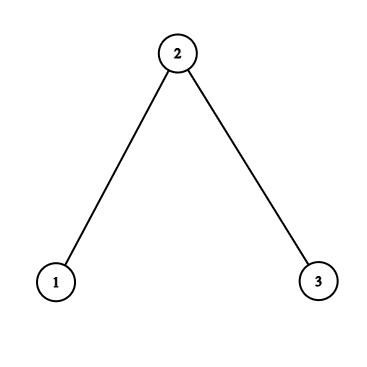In the first test case, only one vertex is in the tree, which is not a leaf, so the answer is $ 0 $ . In the second test case, the tree is shown below. Vertices that have not fallen are denoted in bold. Let us examine the following three cases:  We arrive at this configuration with a probability of $ \left( \frac{1}{2} \right) ^3 $ , where the only unordered pair of distinct leaf vertices is $ (2, 3) $ . 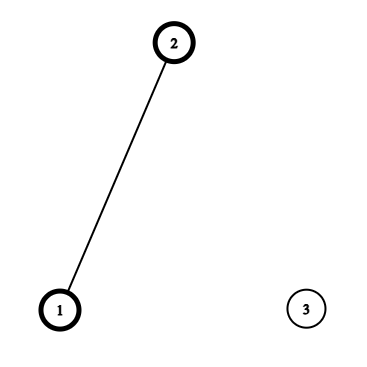 We arrive at this configuration with a probability of $ \left( \frac{1}{2} \right) ^3 $ , where the only unordered pair of distinct leaf vertices is $ (2, 1) $ . 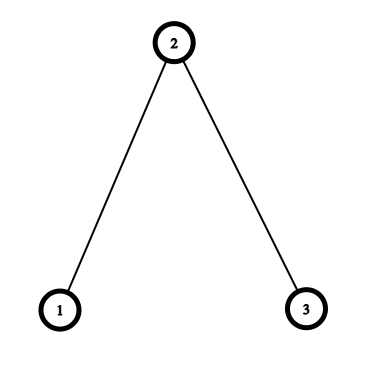 We arrive at this configuration with a probability of $ \left( \frac{1}{2} \right) ^3 $ , where the only unordered pair of distinct leaf vertices is $ (1, 3) $ .All remaining cases contain no unordered pairs of distinct leaf vertices. Hence, the answer is $ \frac{1 + 1 + 1}{8} = \frac{3}{8} $ , which is equal to $ 623\,902\,721 $ modulo $ 998\,244\,353 $ .