CF2074E Empty Triangle

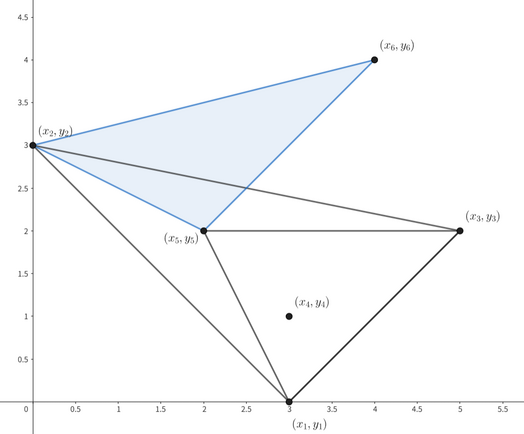
这是一道交互题。 粉色士兵们向你隐藏了 $n$ 个（$3 \le n \le 1500$）固定点 $(x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)$，其坐标未给出。已知任意两点坐标不同，且任意三点不[共线](https://en.wikipedia.org/wiki/Collinearity)。 你可以向主持人（Frontman）询问三个不同的下标 $i$、$j$、$k$。随后，主持人会绘制由点 $(x_i, y_i)$、$(x_j, y_j)$、$(x_k, y_k)$ 构成的三角形，并按以下规则回应： - 若至少有一个隐藏点位于三角形内部，主持人会返回其中一个这样的点的下标。注意，若有多个这样的点，主持人可以任意选择其中一个返回。 - 否则，主持人返回 $0$。  你的目标是找到一个不包含其他隐藏点的三角形（如图中蓝色三角形所示）。你最多可以使用 $\mathbf{75}$ 次询问，找到由三个点构成的、内部不含其他隐藏点的任意三角形。 注意：主持人可能在选择返回的点时具有自适应性。换言之，返回点的选择可能受到多种因素影响（包括但不限于点的排列和之前的询问）。但需注意，点的序列永远不会被改变。 本题禁用 hack。你的解法将在恰好 $\mathbf{35}$ 个输入文件（包括示例输入）上进行评测。

无

每个测试包含多个测试用例。第一行包含测试用例的数量 $t$（$1 \le t \le 20$）。接下来是每个测试用例的描述。 每个测试用例的第一行包含一个正整数 $n$ —— 点的数量（$3 \le n \le 1500$）。 之后，你可以在单独一行输出以下内容进行询问： - "? i j k"（$1 \le i,j,k \le n$，$i \ne j$，$i \ne k$，$j \ne k$）：询问由 $(x_i, y_i)$、$(x_j, y_j)$、$(x_k, y_k)$ 构成的三角形。 随后，交互器会在新的一行返回一个整数： - 若你的询问无效或询问次数超过 $\mathbf{75}$ 次，交互器返回 $-1$； - 若存在下标 $p$（$1 \le p \le n$）使得点 $(x_p, y_p)$ 位于三角形内部，则返回任意一个这样的下标 $p$； - 否则，交互器返回 $0$。 若你想提交答案，可以在单独一行输出以下内容： - "! i j k"（$1 \le i,j,k \le n$，$i \ne j$，$i \ne k$，$j \ne k$）：表示由 $(x_i, y_i)$、$(x_j, y_j)$、$(x_k, y_k)$ 构成的三角形内部不含其他隐藏点。 随后，以下交互会发生： - 若答案无效或三角形包含其他隐藏点，交互器返回 $-1$； - 若答案正确且仍有未处理的测试用例，你将获得下一个测试用例的 $n$ 值； - 否则，表示所有测试用例已正确解决，你的程序可正常终止。 注意：提交答案不计入询问次数。 注意：交互器可能在选择返回的点时具有自适应性。换言之，返回点的选择可能受到多种因素影响（包括但不限于点的排列和之前的询问）。但需注意，点的序列永远不会被改变。 每次输出询问后，请勿忘记换行并刷新$^{\text{∗}}$输出缓冲区。否则，你将收到 Idleness limit exceeded 的判定结果。 若在交互过程中读取到 $-1$ 而非有效数据，你的程序必须立即终止。这意味着你的程序将因无效询问或其他错误被判定为 Wrong answer。未能终止可能导致任意判定结果，因为程序会继续从已关闭的流中读取数据。 Hacks 本题禁用 hack。你的解法将在恰好 $\mathbf{35}$ 个输入文件（包括示例输入）上进行评测。 $^{\text{∗}}$ 刷新缓冲区的方法： - C++ 使用 `fflush(stdout)` 或 `cout.flush()`； - Python 使用 `sys.stdout.flush()`； - 其他语言请参考文档。

第一个测试用例中的点为 $(3,0),(0,3),(5,2),(3,1),(2,2),(4,4)$。 三次询问对应的三角形如下：  可以看到，由 $(0,3)$、$(2,2)$、$(4,4)$ 构成的三角形内部不含其他隐藏点，因此是一个有效答案。 注意：交互示例仅展示合法的交互流程，不一定是实际响应。例如，当查询 "? 1 2 3" 时，主持人可能返回 $4$。但由于主持人不会改变点的序列，因此不会对同一查询返回 $6$。 第二个测试用例中仅有 $3$ 个点。因此，由这三点构成的唯一三角形内部不含其他隐藏点。 翻译由 DeepSeek R1 完成