CF2077E Another Folding Strip

对于一个长度为 $m$ 的数组 $b$，定义 $f(b)$ 如下： 考虑一个 $1 \times m$ 的纸带，所有单元格初始暗度为 $0$。你需要通过以下操作将其转化为第 $i$ 个位置的暗度为 $b_i$ 的纸带。每次操作包含两个步骤： 1. 在任意两个单元格之间的线上折叠纸带。你可以进行任意次折叠（包括不折叠）。 2. 选择一个位置滴下黑色染料。染料会从顶部渗透并向下流动，使其路径上所有单元格的暗度增加 $1$。滴完染料后展开纸带。 令 $f(b)$ 为达成目标配置所需的最小操作次数。可以证明总能通过有限次操作达成目标。 给定一个长度为 $n$ 的数组 $a$，计算 $$ \sum_{l=1}^n\sum_{r=l}^n f(a_l a_{l+1} \ldots a_r) $$ 模 $998\,244\,353$ 的结果。

每个测试包含多个测试用例。第一行输入测试用例数量 $t$（$1 \le t \le 10^4$）。接下来描述每个测试用例。 每个测试用例的第一行输入一个整数 $n$（$1 \leq n \leq 2 \cdot 10^5$）——数组 $a$ 的长度。 第二行输入 $n$ 个整数 $a_1, a_2, \ldots, a_n$（$0 \leq a_i \leq 10^9$）——表示数组 $a$。 保证所有测试用例的 $n$ 总和不超过 $2 \cdot 10^5$。

对于每个测试用例，输出一个整数——所求结果模 $998\,244\,353$ 的值。

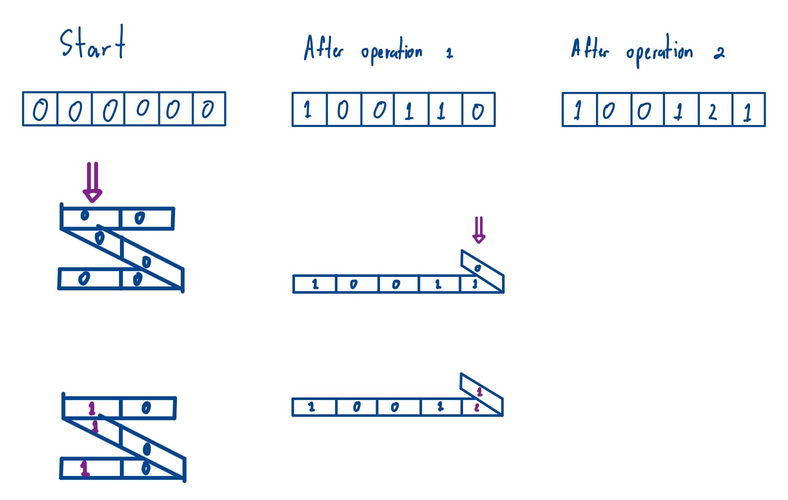
第一个测试用例中： - $f(a_1)=f(\mathtt{0})=0$ - $f(a_1a_2)=f(\mathtt{01})=1$ - $f(a_1a_2a_3)=f(\mathtt{010})=1$ - $f(a_2)=f(\mathtt{1})=1$ - $f(a_2a_3)=f(\mathtt{10})=1$ - $f(a_3)=f(\mathtt{0})=0$ 总和为 $0+1+1+1+1+0 = 4$。 第二个测试用例中，$f(a_1a_2a_3a_4a_5a_6) = 2$。下图展示了一种可能的操作序列：  翻译由 DeepSeek R1 完成