CF207A3 Beaver's Calculator 1.0

The Smart Beaver from ABBYY has once again surprised us! He has developed a new calculating device, which he called the "Beaver's Calculator $ 1.0 $ ". It is very peculiar and it is planned to be used in a variety of scientific problems. To test it, the Smart Beaver invited $ n $ scientists, numbered from $ 1 $ to $ n $ . The $ i $ -th scientist brought $ k_{i} $ calculating problems for the device developed by the Smart Beaver from ABBYY. The problems of the $ i $ -th scientist are numbered from $ 1 $ to $ k_{i} $ , and they must be calculated sequentially in the described order, since calculating each problem heavily depends on the results of calculating of the previous ones. Each problem of each of the $ n $ scientists is described by one integer $ a_{i,j} $ , where $ i $ ( $ 1

The first line contains integer $ n $ — the number of scientists. To lessen the size of the input, each of the next $ n $ lines contains five integers $ k_{i} $ , $ a_{i,1} $ , $ x_{i} $ , $ y_{i} $ , $ m_{i} $ ( $ 0

On the first line print a single number — the number of "bad" pairs in the optimal order. If the total number of problems does not exceed $ 200000 $ , also print 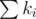 lines — the optimal order of the problems. On each of these lines print two integers separated by a single space — the required number of resources for the problem and the number of the scientist who offered this problem, respectively. The scientists are numbered from $ 1 $ to $ n $ in the order of input.

In the first sample $ n=2 $ , $ k_{1}=2 $ , $ a_{1,1}=1 $ , $ a_{1,2}=2 $ , $ k_{2}=2 $ , $ a_{2,1}=3 $ , $ a_{2,2}=4 $ . We've got two scientists, each of them has two calculating problems. The problems of the first scientist require $ 1 $ and $ 2 $ resource units, the problems of the second one require $ 3 $ and $ 4 $ resource units. Let's list all possible variants of the calculating order (each problem is characterized only by the number of resource units it requires): $ (1,2,3,4) $ , $ (1,3,2,4) $ , $ (3,1,2,4) $ , $ (1,3,4,2) $ , $ (3,4,1,2) $ , $ (3,1,4,2) $ . Sequence of problems $ (1,3,2,4) $ has one "bad" pair ( $ 3 $ and $ 2 $ ), $ (3,1,4,2) $ has two "bad" pairs ( $ 3 $ and $ 1 $ , $ 4 $ and $ 2 $ ), and $ (1,2,3,4) $ has no "bad" pairs.