CF2090C Dining Hall

在一个庞大的王国中，有一个无限大的餐厅。 该餐厅可以表示为由单元格 $(x, y)$ 构成的集合，其中 $x, y$ 是自然数。餐厅内还有无数张桌子。每张桌子由四个单元格定义：$(3x + 1, 3y + 1)$、$(3x + 1, 3y + 2)$、$(3x + 2, 3y + 1)$、$(3x + 2, 3y + 2)$，其中 $x, y$ 是非负整数。所有不属于任何桌子的单元格被视为走廊。 客人只能在走廊中移动，且每次只能通过相邻的边移动到相邻的单元格，每次移动耗时相同。注意：客人只能在最后一次移动时坐在桌子上，且必须坐在桌子上。 在王国的一场晚宴中，共有 $n$ 位客人到来，每位客人有一个特征值 $t_i$（取值为 $0$ 或 $1$）。他们按顺序进入大厅，从单元格 $(0, 0)$ 出发走向某张桌子。若第 $i$ 位客人的 $t_i = 1$，则他会选择距离最近的仍有空位的桌子；若 $t_i = 0$，则他会选择距离最近的未被占用的桌子（即使后续可能有其他客人加入）。若存在多张桌子距离相同，则选择 $x$ 坐标最小的单元格；若仍有多个选项，则选择其中 $y$ 坐标最小的单元格。 从单元格到桌子的距离定义为到该桌子上最近的未被占用的单元格的距离。两单元格之间的距离按移动到相邻单元格的次数计算。注意：移动过程中不允许穿过属于桌子的单元格，除非是最后一步（该步骤会将你放置在桌子的最终单元格上）。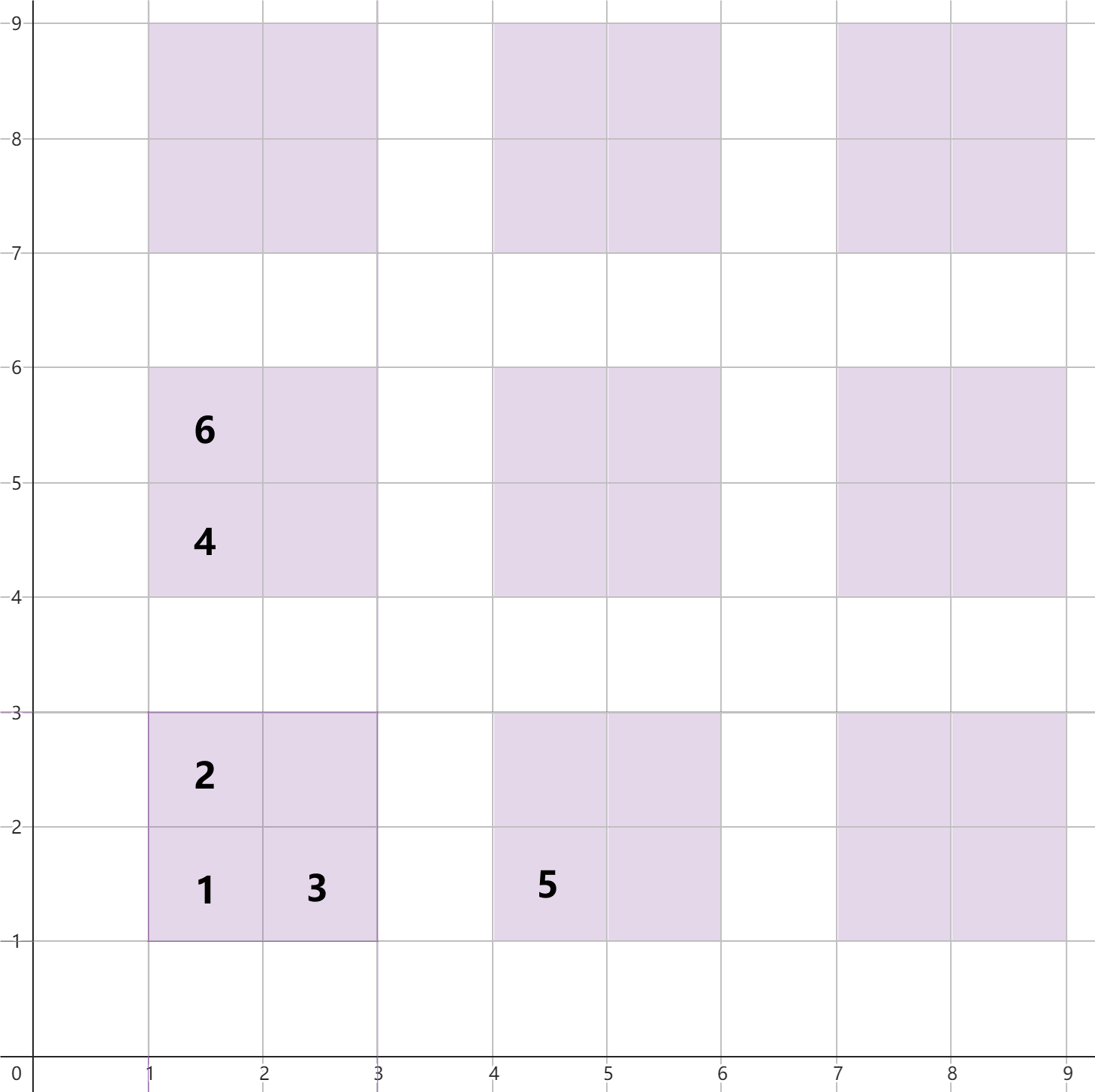 为更好理解条件，可参考说明中的图示。 你无需亲自计算所有客人的入座情况，请直接输出每位客人最终入座的单元格。

第一行包含一个整数 $q$（$1 \leq q \leq 5000$）——测试用例数量。接下来是测试用例描述。 每个测试用例的第一行包含一个整数 $n$（$1 \leq n \leq 50\,000$）——客人数量。 每个测试用例的第二行包含 $n$ 个整数 $t_1, t_2, \ldots, t_n$（$t_i \in \{0, 1\}$）——每位客人的特征值。 保证所有测试用例的 $n$ 之和不超过 $50\,000$。

对于每个测试用例，输出 $n$ 行——每位客人入座的单元格。

第一位客人到单元格 $(1, 1)$ 的距离为 2，因此选择该位置。 第二位客人到单元格 $(1, 2)$ 和 $(2, 1)$ 的距离均为 3，但由于 $1 < 2$，因此选择 $(1, 2)$。无额外约束。 第三位客人到单元格 $(2, 1)$ 的距离为 3，因此选择该位置。 第四位客人到单元格 $(1, 4)$ 的距离为 5，因此选择该位置。 第五位客人到单元格 $(4, 1)$ 的距离为 5。 第六位客人到单元格 $(1, 5)$ 和 $(2, 2)$ 的距离均为 6，但由于 $x$ 坐标更小，因此选择 $(1, 5)$。  翻译由 DeepSeek R1 完成