CF2092E She knows...

D. Pippy 正在为家中的"黑白派对"做准备。他只需要重新粉刷地下室的地板，地板可表示为 $n \times m$ 的棋盘。 在上次派对后，整个棋盘除 $k$ 个单元格 $(x_1, y_1), (x_2, y_2), \ldots, (x_k, y_k)$ 外均被涂成绿色，这些单元格已被涂成白色或黑色。为了即将到来的派对，D. Pippy 想要将剩余的绿色单元格涂成黑色或白色。同时，他要求重新粉刷后棋盘上相邻颜色不同的单元格对数量为偶数。 形式化地，若定义集合： $$A = \left\{((i_1, j_1), (i_2, j_2)) \ | \ 1 \le i_1, i_2 \le n, 1 \le j_1, j_2 \le m, i_1+j_1 < i_2+j_2, |i_1-i_2|+|j_1-j_2| = 1, \operatorname{color}(i_1, j_1) \neq \operatorname{color}(i_2, j_2) \right\},$$ 其中 $\operatorname{color}(x, y)$ 表示单元格 $(x, y)$ 的颜色，则要求 $|A|$ 为偶数。 请帮助 D. Pippy 计算满足条件的粉刷方案数。由于答案可能很大，请输出其对 $10^9 + 7$ 取模的结果。

每个测试包含多个测试用例。输入数据第一行包含一个整数 $t$ ($1 \le t \le 10^4$) —— 测试用例数量。接下来是测试用例描述。 每个测试用例的第一行包含三个整数 $n, m, k$ ($3 \le n, m \le 10^9$; $1 \le k \le 2 \cdot 10^5$) —— 棋盘的尺寸和初始非绿色单元格的数量。 接下来每个测试用例的 $k$ 行中，第 $i$ 行包含三个整数 $x_i, y_i$ 和 $c_i$ ($1 \le x_i \le n$; $1 \le y_i \le m$; $c_i \in \{0, 1\}$) —— 单元格的坐标及其颜色（白色对应 $c_i = 0$，黑色对应 $c_i = 1$）。保证所有单元格坐标互不相同。 保证所有测试用例的 $k$ 之和不超过 $2 \cdot 10^5$。

对于每个测试用例，输出一个整数 —— 答案对 $10^9 + 7$ 取模的结果。

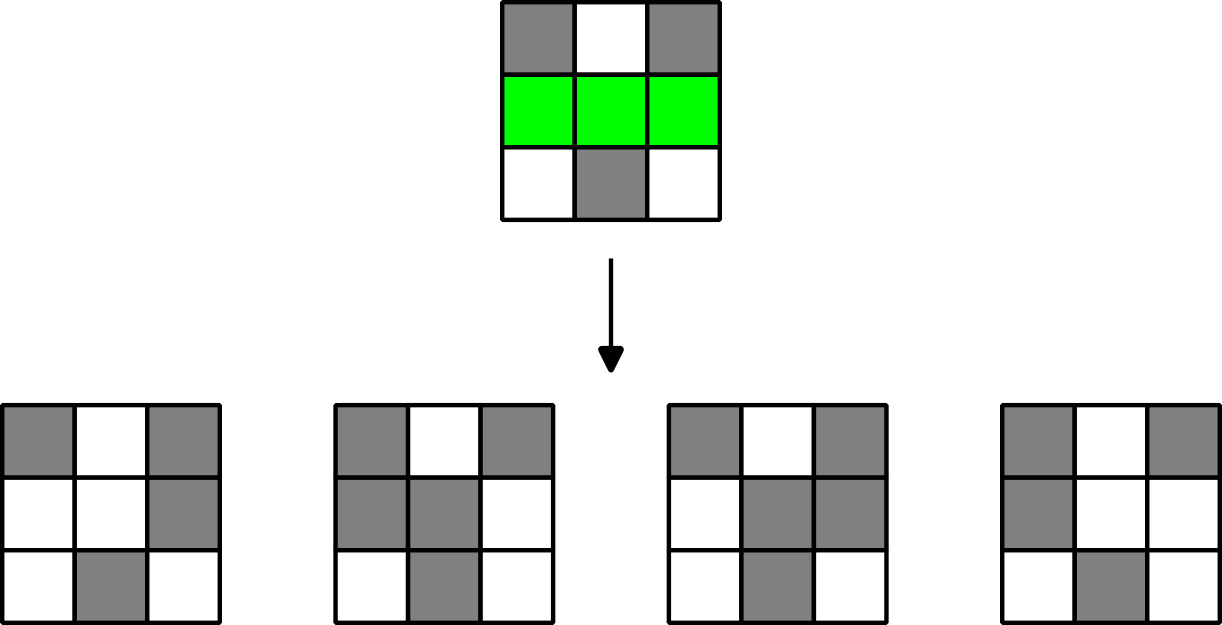
第一个测试案例中，绿色单元格 $(2, 1), (2, 2), (2, 3)$ 共有 $4$ 种合法涂色方案，分别为：$(1, 1, 0)$，$(0, 0, 1)$，$(1, 0, 0)$，$(0, 1, 1)$（颜色按单元格顺序排列），如下图所示。  第二个测试案例中，棋盘已全部涂色且相邻异色对数量为奇数，因此答案为 $0$。 翻译由 DeepSeek R1 完成