CF2097C Bermuda Triangle

百慕大三角——大西洋中一片神秘区域，据传言船只和飞机都会在此凭空消失。有人归咎于磁力异常，有人则认为是通往异世界的传送门，但真相仍笼罩在谜团之中。 在一个晴朗的日子里，814 次常规客运航班正从迈阿密飞往拿骚。在飞机进入一片诡异闪烁的迷雾区域前，一切都看似正常。无线电通讯中断，仪表疯狂旋转，窗外闪烁着非自然的光芒。 为简化问题，我们假设百慕大三角和飞机都位于平面上，且三角形的顶点坐标为 $(0, 0)$、$(0, n)$ 和 $(n, 0)$。飞机初始位于严格处于百慕大三角内部的点 $(x, y)$，并以速度向量 $(v_x, v_y)$ 移动。由于所有仪器都已失灵，机组人员无法控制飞机。 当飞机到达三角形任意一个顶点时，即可成功逃离。但如果飞机在任意时刻（可能是非整数时间）碰到三角形的边界（不包括顶点），其速度向量会立即根据该边进行镜面反射$^\dagger$，随后飞机将继续沿新方向移动。 请判断飞机是否能逃离百慕大三角（即到达某个顶点）。如果可能，还需计算在逃离前会碰到边界的次数（每次触碰边界都计入次数，即使是在同一点；经过顶点不计入次数）。 $^\dagger$ 反射遵循物理定律：入射角等于反射角。

每个测试包含多个测试用例。第一行输入测试用例数量 $t$（$1 \le t \le 10^4$）。接下来是各测试用例的描述。 每个测试用例的唯一一行包含五个整数 $n$、$x$、$y$、$v_x$ 和 $v_y$（$3 \le n \le 10^9$，$1 \le x, y$，$x+y < n$，$1 \le v_x, v_y \le 10^9$）——分别描述三角形的顶点坐标、飞机的初始位置和初始速度向量。

对于每个测试用例，输出一个整数——飞机逃离前触碰边界的次数。如果飞机永远无法逃离，则输出 $-1$。

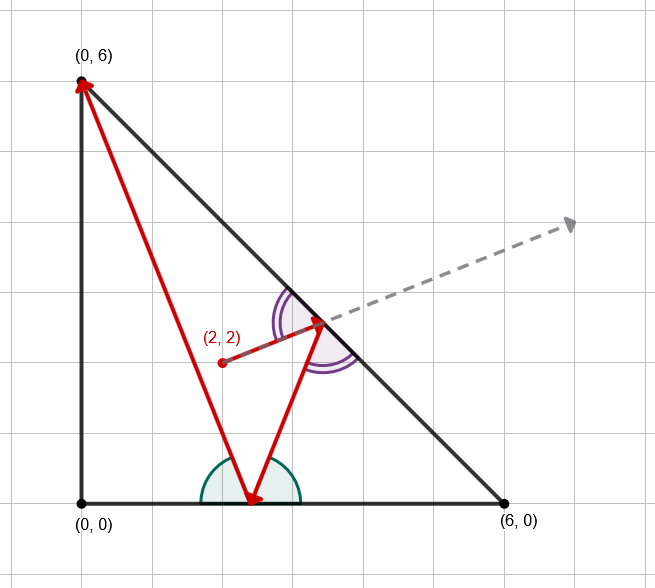
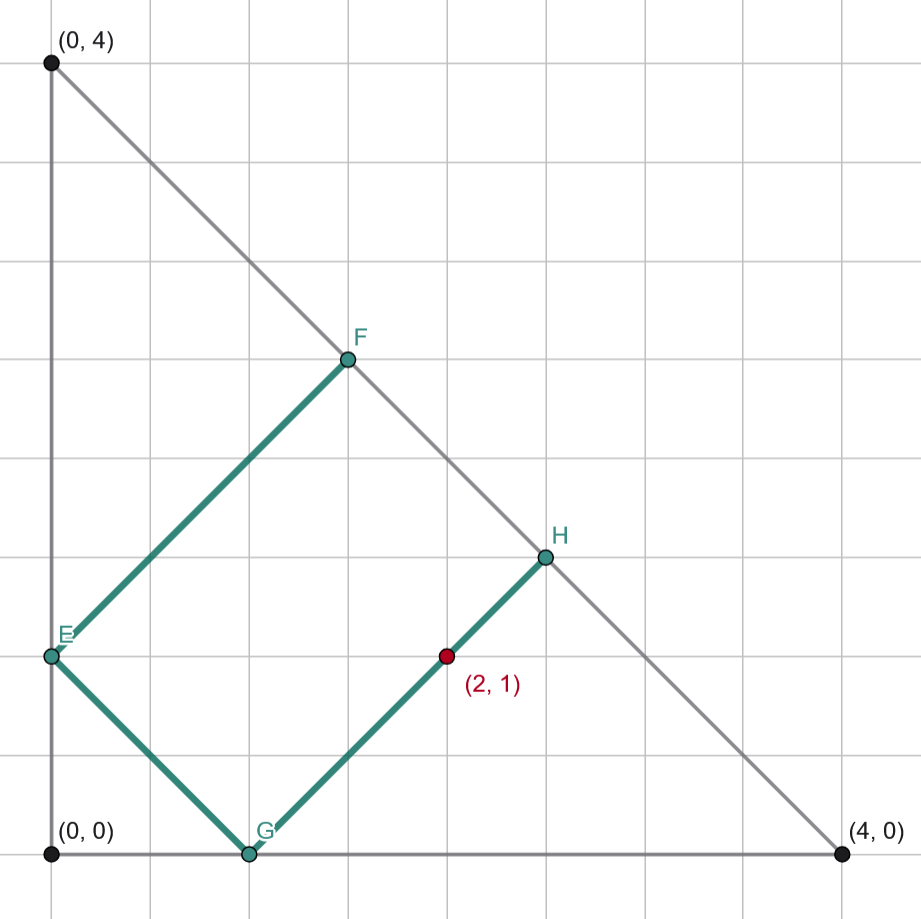
第一个测试用例的示意图如下：  第二个测试用例中，除速度外初始数据与第一个测试用例相同，且飞机初始运动方向相同，因此答案相同。 第三个测试用例的答案为 $-1$，因为飞机将始终沿着绿色标记的线段移动。示意图如下：  翻译由 DeepSeek V3 完成