CF2101E Kia Bakes a Cake

给定一个长度为 $n$ 的二进制字符串 $s$ 和一棵包含 $n$ 个顶点的树 $T$。设 $k$ 为 $s$ 中字符 $\mathtt{1}$ 的数量。我们将按照以下规则构造一个包含 $k$ 个顶点的完全无向加权图： - 对于每个满足 $s_i = \mathtt{1}$ 的 $1 \le i \le n$，创建一个标记为 $i$ 的顶点。 - 对于在上述步骤中创建的任意两个标记为 $u$ 和 $v$ 的顶点，定义它们之间的边权 $w(u, v)$ 为顶点 $u$ 和顶点 $v$ 在树 $T$ 中的距离 $^{\text{∗}}$。 一个依次访问标记为 $v_1, v_2, \ldots, v_m$ 的顶点的简单路径 $^{\text{†}}$ 被称为"优美的"，如果对于所有 $1 \le i \le m - 2$，满足条件 $2 \cdot w(v_i, v_{i + 1}) \le w(v_{i + 1}, v_{i + 2})$。换句话说，路径中每条边的权值必须至少是前一条边权值的两倍。注意对于所有 $1 \le i \le m$，必须满足 $s_{v_i} = \mathtt{1}$，否则将不存在对应标记的顶点。 对于完全无向加权图中每个标记为 $i$ 的顶点（$1 \le i \le n$ 且 $s_i = \mathtt{1}$），确定从该顶点出发的所有优美简单路径中包含顶点的最大数量。 $^{\text{∗}}$ 树中两个顶点 $a$ 和 $b$ 之间的距离等于顶点 $a$ 和顶点 $b$ 之间唯一简单路径上的边数。 $^{\text{†}}$ 路径是指顶点序列 $v_1, v_2, \ldots, v_m$，其中对于所有 $1 \le i \le m - 1$，$v_i$ 和 $v_{i + 1}$ 之间存在一条边。简单路径是指没有重复顶点的路径，即对于所有 $1 \le i < j \le m$，$v_i \neq v_j$。

每个测试包含多个测试用例。第一行输入测试用例数量 $t$（$1 \le t \le 10^4$）。接下来是各测试用例的描述。 每个测试用例的第一行包含一个整数 $n$（$1 \le n \le 7 \cdot 10^4$）——二进制字符串 $s$ 的长度和树 $T$ 的顶点数。 第二行包含一个由 $n$ 个字符组成的二进制字符串 $s_1s_2\ldots s_n$（$s_i \in \{\mathtt{0}, \mathtt{1}\}$）——表示要在完全无向加权图中构造顶点的字符串。 接下来的 $n - 1$ 行，每行包含两个整数 $u$ 和 $v$（$1 \le u, v \le n$）——树 $T$ 的边的端点。 保证给定的边构成一棵树。 保证所有测试用例的 $n$ 之和不超过 $7 \cdot 10^4$。

对于每个测试用例，输出 $n$ 个整数，第 $i$ 个整数表示从标记为 $i$ 的顶点出发的所有优美简单路径中包含顶点的最大数量。如果不存在标记为 $i$ 的顶点（即 $s_i = \mathtt{0}$），则输出 $-1$。

在第一个测试用例中，树 $T$ 和构造的图如下所示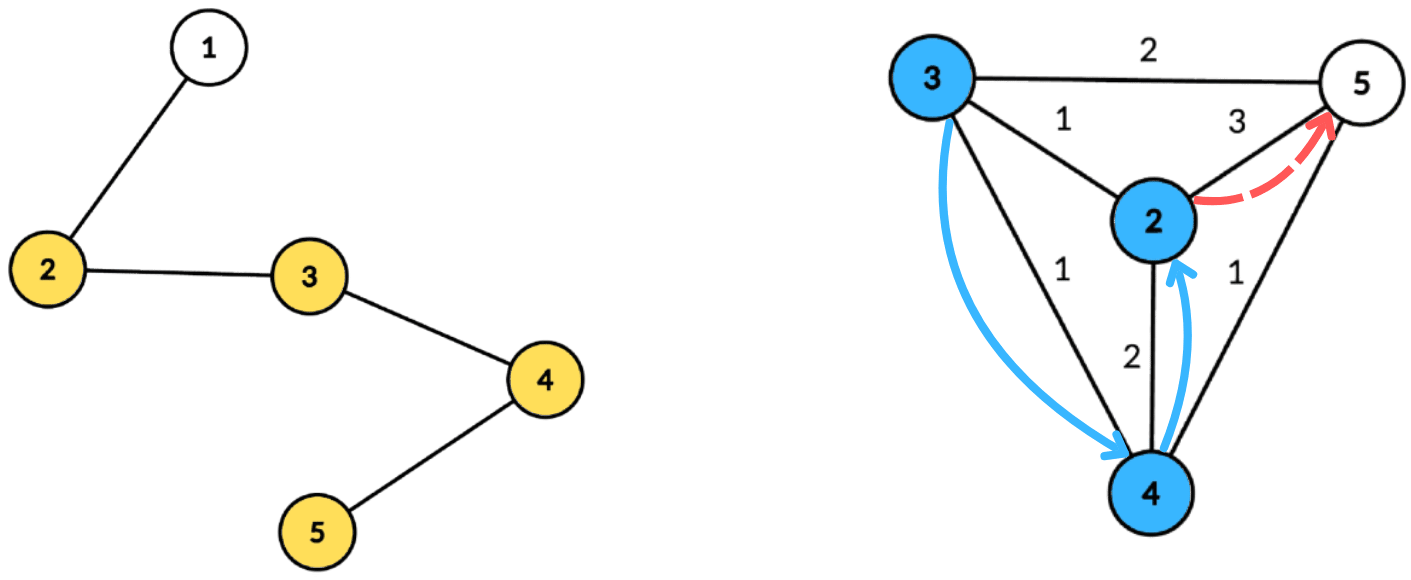：  左侧是树 $T$，选中的节点标记为黄色。右侧是构造的完全图。图中展示的优美路径是 $3\rightarrow 4\rightarrow 2$。该路径是优美的，因为 $w(4, 2) = 2$ 至少是 $w(3, 4) = 1$ 的两倍。尝试用 $2\rightarrow 5$ 扩展路径是不可行的，因为 $w(2, 5) = 3$ 小于 $w(4, 2) = 2$ 的两倍。 在第二个测试用例中，树 $T$ 是一条长度为 $17$ 的简单路径。从标记为 $2$ 的顶点出发的一个优美路径示例是 $2\rightarrow 3\rightarrow 5\rightarrow 9\rightarrow 17$，其边权依次为 $1, 2, 4, 8$，每次翻倍。 翻译由 DeepSeek V3 完成