CF2101E Kia Bakes a Cake

You are given a binary string $ s $ of length $ n $ and a tree $ T $ with $ n $ vertices. Let $ k $ be the number of 1s in $ s $ . We will construct a complete undirected weighted graph with $ k $ vertices as follows: - For each $ 1\le i\le n $ with $ s_i = \mathtt{1} $ , create a vertex labeled $ i $ . - For any two vertices labeled $ u $ and $ v $ that are created in the above step, define the edge weight between them $ w(u, v) $ as the distance $ ^{\text{∗}} $ between vertex $ u $ and vertex $ v $ in the tree $ T $ . A simple path $ ^{\text{†}} $ that visits vertices labeled $ v_1, v_2, \ldots, v_m $ in this order is nice if for all $ 1\le i\le m - 2 $ , the condition $ 2\cdot w(v_i, v_{i + 1})\le w(v_{i + 1}, v_{i + 2}) $ holds. In other words, the weight of each edge in the path must be at least twice the weight of the previous edge. Note that $ s_{v_i} = \mathtt{1} $ has to be satisfied for all $ 1\le i\le m $ , as otherwise, there would be no vertex with the corresponding label. For each vertex labeled $ i $ ( $ 1\le i\le n $ and $ s_i = \mathtt{1} $ ) in the complete undirected weighted graph, determine the maximum number of vertices in any nice simple path starting from the vertex labeled $ i $ . $ ^{\text{∗}} $ The distance between two vertices $ a $ and $ b $ in a tree is equal to the number of edges on the unique simple path between vertex $ a $ and vertex $ b $ . $ ^{\text{†}} $ A path is a sequence of vertices $ v_1, v_2, \ldots, v_m $ such that there is an edge between $ v_i $ and $ v_{i + 1} $ for all $ 1\le i\le m - 1 $ . A simple path is a path with no repeated vertices, i.e., $ v_i\neq v_j $ for all $ 1\le i < j\le m $ .

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 10^4 $ ). The description of the test cases follows. The first line of each test case contains a single integer $ n $ ( $ 1\le n\le 7\cdot10^4 $ ) — the length of the binary string $ s $ and the number of vertices in the tree $ T $ . The second line of each test case contains a binary string with $ n $ characters $ s_1s_2\ldots s_n $ ( $ s_i\in \{\mathtt{0}, \mathtt{1}\} $ ) — the string representing the vertices to be constructed in the complete undirected weighted graph. Each of the next $ n - 1 $ lines contains two integers $ u $ and $ v $ ( $ 1\le u, v\le n $ ) — the endpoints of the edges of the tree $ T $ . It is guaranteed that the given edges form a tree. It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 7\cdot10^4 $ .

For each test case, output $ n $ integers, the $ i $ -th integer representing the maximum number of vertices in any nice simple path starting from the vertex labeled $ i $ . If there is no vertex labeled $ i $ , i.e., $ s_i = \mathtt{0} $ , output $ -1 $ instead.

In the first test case, the tree $ T $ and the constructed graph are as follows: 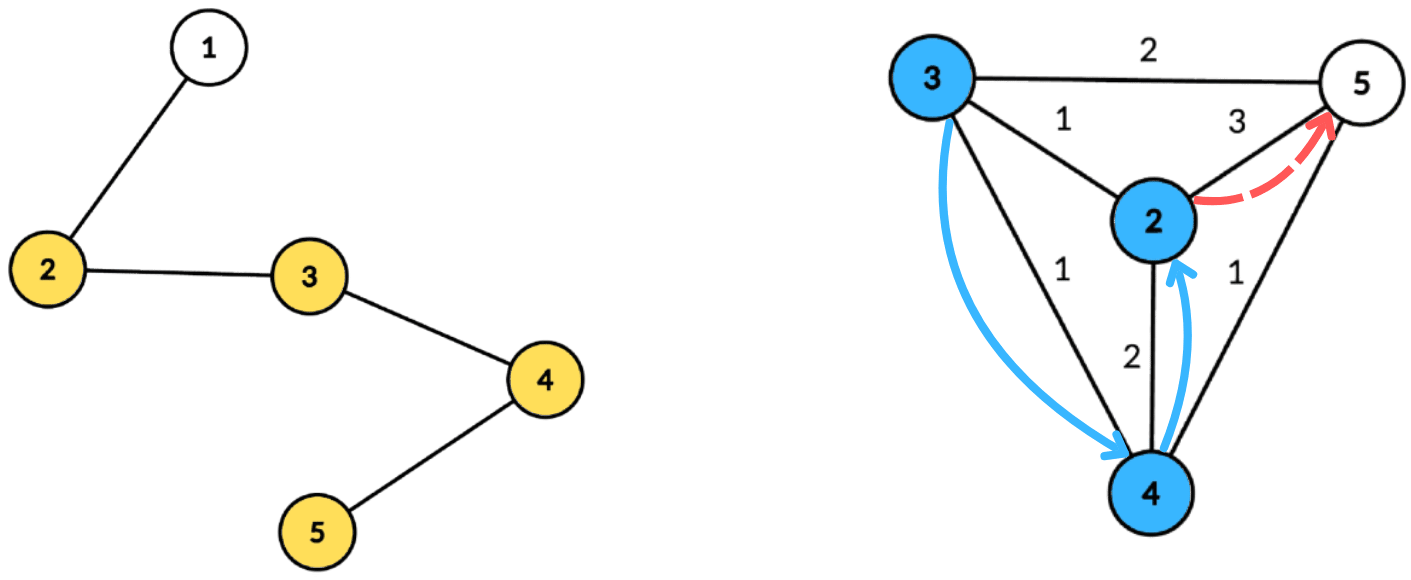 Left side is the tree $ T $ with selected nodes colored yellow. The right side is the constructed complete graph.The nice path shown in the diagram is $ 3\rightarrow 4\rightarrow 2 $ . The path is nice as $ w(4, 2) = 2 $ is at least twice of $ w(3, 4) = 1 $ . Extending the path using $ 2\rightarrow 5 $ is not possible as $ w(2, 5) = 3 $ is less than twice of $ w(4, 2) = 2 $ . In the second test case, the tree $ T $ is a simple path of length $ 17 $ . An example of a nice path starting from the vertex labeled $ 2 $ is $ 2\rightarrow 3\rightarrow 5\rightarrow 9\rightarrow 17 $ , which has edge weights of $ 1, 2, 4, 8 $ doubling each time.