CF2101F Shoo Shatters the Sunshine

给定一棵包含 $n$ 个顶点的树，每个顶点可以被染成红色、蓝色或白色。一种染色方案的"酷度"定义为红色顶点和蓝色顶点之间的最大距离 $^{\text{∗}}$。 形式化地说，如果将第 $i$ 个顶点的颜色记为 $c_i$，则染色方案的酷度为所有满足 $c_u$ 为红色且 $c_v$ 为蓝色的顶点对 $1 \le u, v \le n$ 的 $d(u, v)$ 的最大值。如果不存在红色顶点或蓝色顶点，则酷度为 0。 你的任务是计算所有 $3^n$ 种可能的树染色方案的酷度之和，结果对 $998\,244\,353$ 取模。 $^{\text{∗}}$ 树中两个顶点 $a$ 和 $b$ 之间的距离等于顶点 $a$ 和顶点 $b$ 之间唯一简单路径上的边数。

每个测试包含多个测试用例。第一行输入测试用例数量 $t$（$1 \le t \le 50$）。接下来是各测试用例的描述。 每个测试用例的第一行包含一个整数 $n$（$2 \le n \le 3000$）——树中的顶点数量。 接下来的 $n - 1$ 行，每行包含两个整数 $u$ 和 $v$（$1 \le u, v \le n$）——树的边的端点。 保证给定的边构成一棵树。 保证所有测试用例的 $n$ 之和不超过 $3000$。

对于每个测试用例，输出所有 $3^n$ 种可能的染色方案的酷度之和，结果对 $998\,244\,353$ 取模。

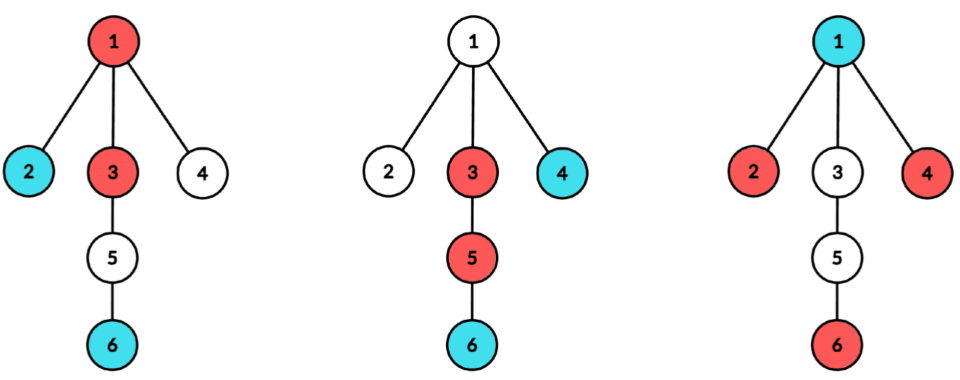
在第一个测试用例中，有 $12$ 种染色方案至少包含一个蓝色顶点和一个红色顶点。下图展示了这些染色方案及其酷度：  所有这些染色方案的酷度为 $2$  所有这些染色方案的酷度为 $1$ 因此，所有可能染色方案的酷度之和为 $6 \cdot 2 + 6 \cdot 1 = 18$。 在第二个测试用例中，以下是酷度为 $3$ 的一些染色方案示例：  翻译由 DeepSeek V3 完成