CF2101F Shoo Shatters the Sunshine

You are given a tree with $ n $ vertices, where each vertex can be colored red, blue, or white. The coolness of a coloring is defined as the maximum distance $ ^{\text{∗}} $ between a red and a blue vertex. Formally, if we denote the color of the $ i $ -th vertex as $ c_i $ , the coolness of a coloring is $ \max d(u, v) $ over all pairs of vertices $ 1\le u, v\le n $ where $ c_u $ is red and $ c_v $ is blue. If there are no red or no blue vertices, the coolness is zero. Your task is to calculate the sum of coolness over all $ 3^n $ possible colorings of the tree, modulo $ 998\,244\,353 $ . $ ^{\text{∗}} $ The distance between two vertices $ a $ and $ b $ in a tree is equal to the number of edges on the unique simple path between vertex $ a $ and vertex $ b $ .

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 50 $ ). The description of the test cases follows. The first line of each test case contains a single integer $ n $ ( $ 2\le n\le 3000 $ ) — the number of vertices in the tree. Each of the next $ n - 1 $ lines contains two integers $ u $ and $ v $ ( $ 1\le u, v\le n $ ) — the endpoints of the edges of the tree. It is guaranteed that the given edges form a tree. It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 3000 $ .

For each test case, output the sum of coolness over all $ 3^n $ possible colorings of the tree, modulo $ 998\,244\,353 $ .

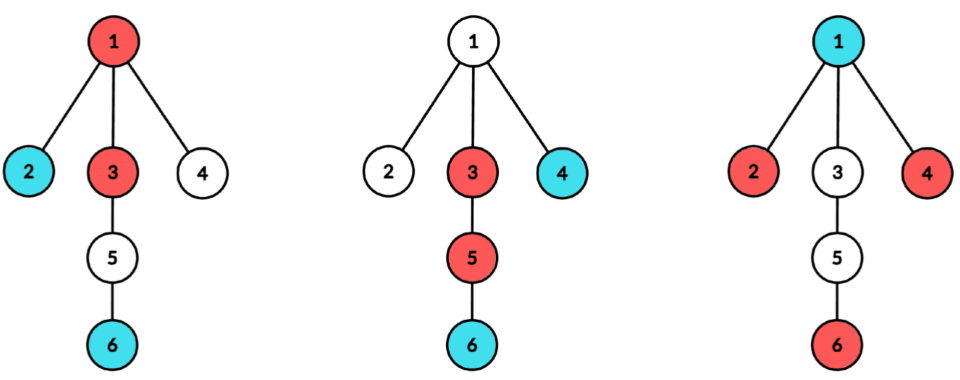
In the first test case, there are $ 12 $ colorings that have at least one blue and one red node. The following pictures show their coloring and their coolness:  All these colorings have coolness $ 2 $  All these colorings have coolness $ 1 $ Therefore, the sum of coolness over all possible colorings is $ 6\cdot 2 + 6\cdot 1 = 18 $ . In the second test case, the following are some examples of colorings with a coolness of $ 3 $ :