CF2108E Spruce Dispute

四月的天气已经相当炎热，Polycarp 决定这是拆除他几年前搭建的云杉树的绝佳时机。当他绕着树走了几个小时，积蓄力量时，他注意到一个有趣的现象：这棵云杉实际上是一棵树$^{\text{∗}}$——而且不是普通的树，它由奇数个顶点 $n$ 组成。更特别的是，$n-1$ 个顶点上挂着圣诞装饰品，这些装饰品恰好涂有 $\frac{n-1}{2}$ 种不同的颜色，每种颜色恰好有两个装饰品。剩下的顶点按照传统，挂着树顶的星星。 经过几天的心理准备，Polycarp 终于开始拆除云杉。他先取下了树顶的星星，并开始拆卸一些树枝，这时他突然想到一个自然的问题：如何移除树的一条边，并重新排列装饰品，使得同色装饰品之间的简单路径长度之和尽可能大？ 在这个问题中，移除树的一条边的定义如下：选择一对相邻顶点 $a$ 和 $b$（$a < b$），然后从树中移除顶点 $b$，并将 $b$ 的所有相邻顶点（除了 $a$）直接重新连接到 $a$ 上。 Polycarp 在得到这个问题的答案之前无法继续拆除云杉。然而，检查所有可能的选项会花费他数年时间。鉴于你在竞赛编程方面的经验，他向你求助。但你能解决这个争议吗？ $^{\text{∗}}$ 树是指一个无环的连通图。

每个测试包含多个测试用例。第一行包含测试用例的数量 $t$（$1 \le t \le 10^4$）。接下来是测试用例的描述。 每个测试用例的第一行包含一个奇数 $n$（$3 \le n < 2 \cdot 10^5$）——树中顶点的数量。 接下来的 $n-1$ 行描述了树的边，每行给出两个相邻顶点 $u$ 和 $v$（$1 \le u, v \le n$，$u \neq v$）。 保证所有测试用例的 $n$ 之和不超过 $2 \cdot 10^5$。

对于每个测试用例，你需要输出两行。 第一行输出一对顶点 $u$ 和 $v$，表示 Polycarp 将要移除的边。 第二行输出一个长度为 $n$ 的数组 $c$，其中 $c[i]$ 表示顶点 $i$ 被分配的正颜色编号（从 $0$ 到 $\frac{n-1}{2}$）。注意，$c[\text{max}(u, v)]$ 必须为 $0$，因为该顶点已被移除。

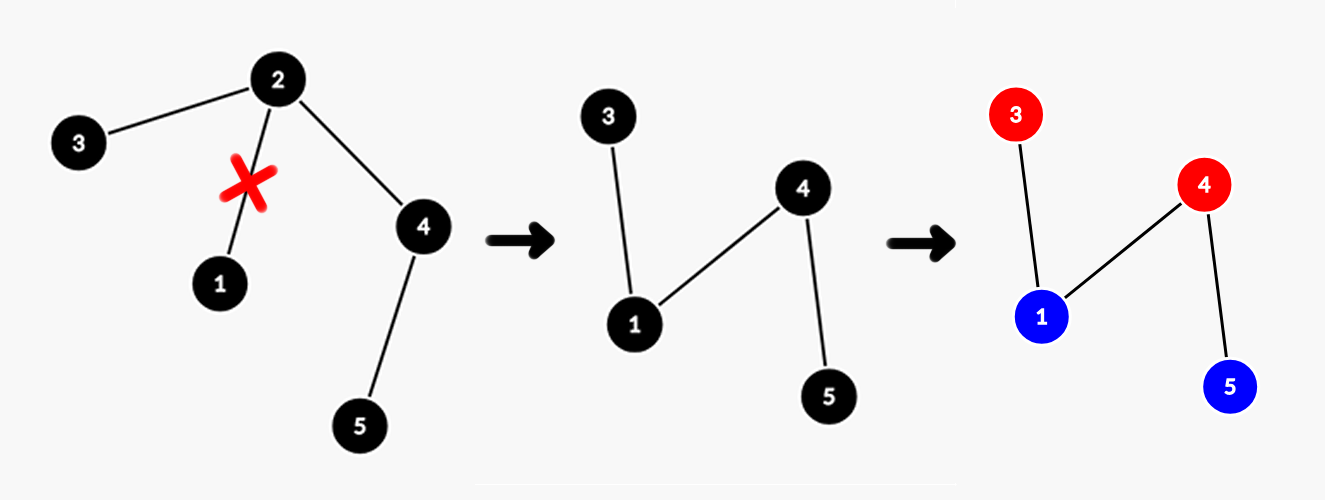
考虑第一个测试用例。 移除连接顶点 $1$ 和 $2$ 的边。之后，顶点 $2$ 将从树中移除，顶点 $3$ 和 $4$ 将被连接到顶点 $1$。 将顶点 $3$ 和 $4$ 涂为第一种颜色，顶点 $1$ 和 $5$ 涂为第二种颜色。同色装饰品之间的简单路径长度之和为 $2 + 2 = 4$。可以证明，这是可能的最大值。  在第二个和第三个例子中，路径长度之和的最大值分别为 $3$ 和 $9$。 翻译由 DeepSeek V3 完成