CF2108F Fallen Towers

Pizano built an array $ a $ of $ n $ towers, each consisting of $ a_i \ge 0 $ blocks. Pizano can knock down a tower so that the next $ a_i $ towers grow by $ 1 $ . In other words, he can take the element $ a_i $ , increase the next $ a_i $ elements by one, and then set $ a_i $ to $ 0 $ . The blocks that fall outside the array of towers disappear. If Pizano knocks down a tower with $ 0 $ blocks, nothing happens. Pizano wants to knock down all $ n $ towers in any order, each exactly once. That is, for each $ i $ from $ 1 $ to $ n $ , he will knock down the tower at position $ i $ exactly once. Moreover, the resulting array of tower heights must be non-decreasing. This means that after he knocks down all $ n $ towers, for any $ i < j $ , the tower at position $ i $ must not be taller than the tower at position $ j $ . You are required to output the maximum $ \text{MEX} $ of the resulting array of tower heights. The $ \text{MEX} $ of an array is the smallest non-negative integer that is not present in the array.

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 10^4 $ ). The description of the test cases follows. The first line of each test case contains an integer $ n $ ( $ 1 \leq n \leq 10^5 $ ) — the number of towers. The second line of each test case contains $ n $ integers — the initial heights of the towers $ a_1, \ldots, a_n $ ( $ 0 \leq a_i \leq 10^9 $ ). It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 10^5 $ .

For each test case, output a single integer — the maximum $ \text{MEX} $ of the final array.

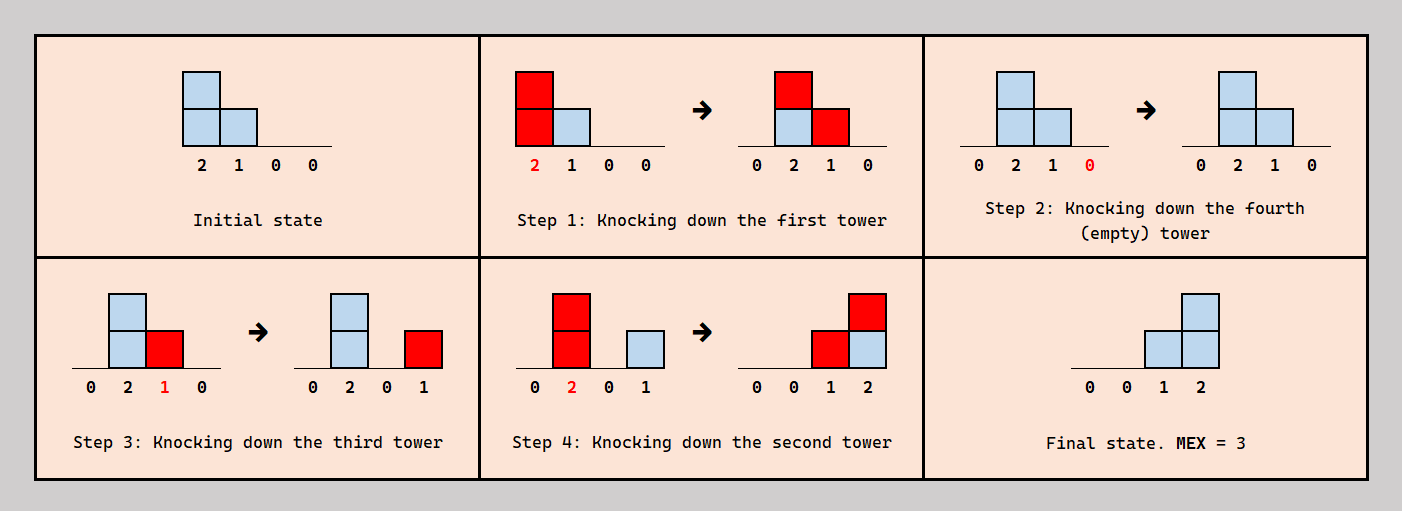
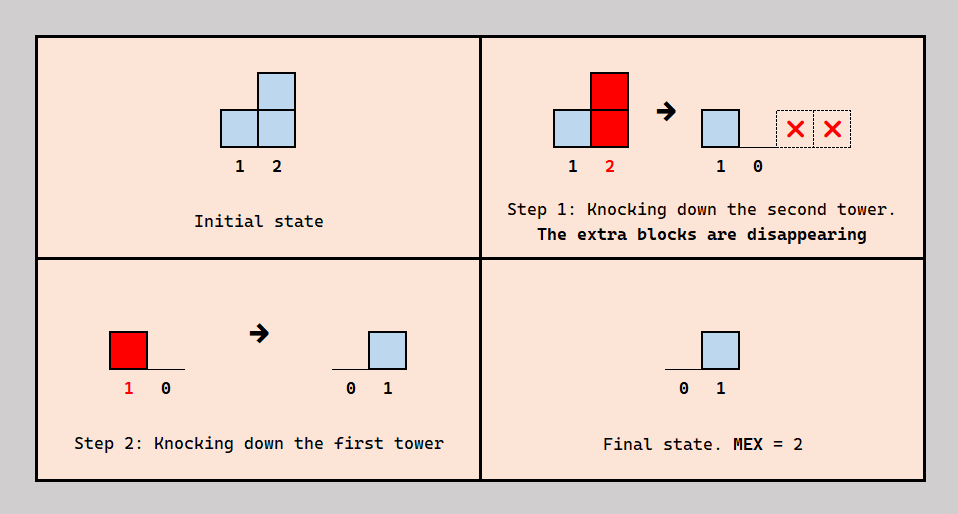Explanation for the first test case. Explanation for the second test case. Note that all towers were knocked down exactly once, and the final array of heights is non-decreasing.