CF2109B Slice to Survive

决斗者 Mouf 和 Fouad 进入了一个 $n \times m$ 的网格竞技场！ Fouad 的怪物初始位于单元格 $(a, b)$，其中行编号为 $1$ 到 $n$，列编号为 $1$ 到 $m$。 Mouf 和 Fouad 将持续决斗，直到网格仅剩一个单元格。 每个回合包含以下操作： - Mouf 首先沿某行或列将网格切割成两部分，丢弃不包含 Fouad 怪物的部分。注意网格必须至少有两个单元格，否则游戏已经结束。 - 之后，在同一回合内，Fouad 将他的怪物移动到剩余网格中的任意单元格（可以保持原位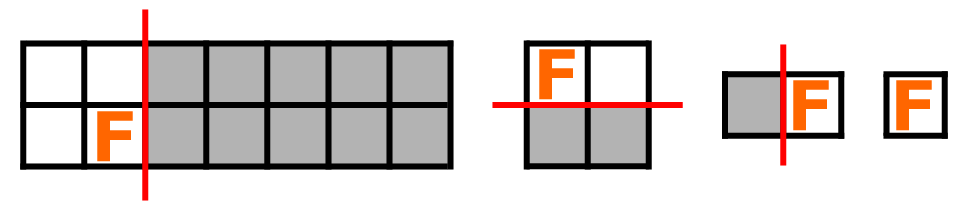）。  第四个测试案例的可视化图示。 Mouf 希望最小化回合数，而 Fouad 希望最大化回合数。如果双方都采取最优策略，这场史诗级决斗将持续多少回合？

每个测试包含多个测试用例。第一行包含测试用例数量 $t$（$1 \le t \le 10^4$）。接下来是测试用例描述。 每个测试用例的第一行也是唯一一行包含四个整数 $n$、$m$、$a$ 和 $b$（$2 \le n, m \le 10^9$，$1 \le a \le n$，$1 \le b \le m$）——分别表示行数、列数、怪物起始行和起始列。

对于每个测试用例，输出一个整数——在双方都采取最优策略时，这场史诗级决斗将持续的回合数。

在第一个测试案例中，一种可能的决斗序列如下： - 第 1 回合：Mouf 沿第 1 行和第 2 行之间的水平线切割网格，移除下半部分，留下 $1 \times 2$ 的网格。 - 第 1 回合：Fouad 的怪物位于单元格 $(1,1)$。 - 第 2 回合：Mouf 再次切割 $1 \times 2$ 网格，移除一列，最终隔离出单元格 $(1,1)$。 决斗在 $2$ 回合内完成。 在第四个测试案例中，一种可能的决斗序列如下： - 第 1 回合：Mouf 沿第 2 列和第 3 列之间的垂直线切割网格，将其分为 $2 \times 2$ 和 $2 \times 5$ 两部分，然后移除 $2 \times 5$ 部分。 - 第 1 回合：Fouad 将怪物移动到单元格 $(1,1)$。 - 此后，决斗过程与第一个测试案例类似——再用两个回合将 $2 \times 2$ 网格缩减为 $1 \times 1$ 单元格。 总计，决斗在 $3$ 回合内完成。 可以参考题目描述中提到的图片来查看第四个测试案例的图示。 翻译由 DeepSeek V3 完成