CF2111B Fibonacci Cubes
题目描述
有 $n$ 个斐波那契立方体,其中第 $i$ 个立方体的边长等于 $f_i$,这里 $f_i$ 是第 $i$ 个斐波那契数。
在这个问题中,斐波那契数的定义如下:
- $f_{1} = 1$
- $f_{2} = 2$
- $f_{i} = f_{i - 1} + f_{i - 2}$ (当 $i > 2$ 时)
还有 $m$ 个空盒子,其中第 $i$ 个盒子的宽度为 $w_i$,长度为 $l_i$,高度为 $h_i$。
对于这 $m$ 个盒子中的每一个,你需要判断是否所有的立方体都能放进这个盒子中。放置立方体必须遵循以下规则:
- 立方体只能堆叠在盒子中,并且立方体的边必须与盒子的边平行;
- 每个立方体必须放在盒子的底部,或者放在其他立方体的顶部,并且放置后该立方体下方空间被完全填满(不能悬空);
- 较大的立方体不能放在较小的立方体顶部。
输入格式
输入包含多个测试用例。第一行包含一个整数 $t$($1 \le t \le 10^{3}$)—— 表示测试用例的数量。接下来是各个测试用例的描述。
每个测试用例的第一行包含两个整数 $n$ 和 $m$($2 \le n \le 10$,$1 \le m \le 2 \cdot 10^{5}$)—— 分别表示立方体的数量和空盒子的数量。
每个测试用例接下来的 $m$ 行,每行包含 $3$ 个整数 $w_i$, $l_i$, $h_i$ ( $1 \le w_i, l_i, h_i \le 150$ ) —— 表示第 $i$ 个盒子的尺寸(宽、长、高)。
输入额外约束:
- 所有测试用例的 $m$ 的总和不超过 $2 \cdot 10^{5}$。
输出格式
对于每个测试用例,输出一个长度为 $m$ 的字符串:如果所有的方块( $n$ 个)都能装入第 $i$ 个盒子,则该字符串的第 $i$ 个字符为 `1`;否则第 $i$ 个字符为 `0`。
说明/提示
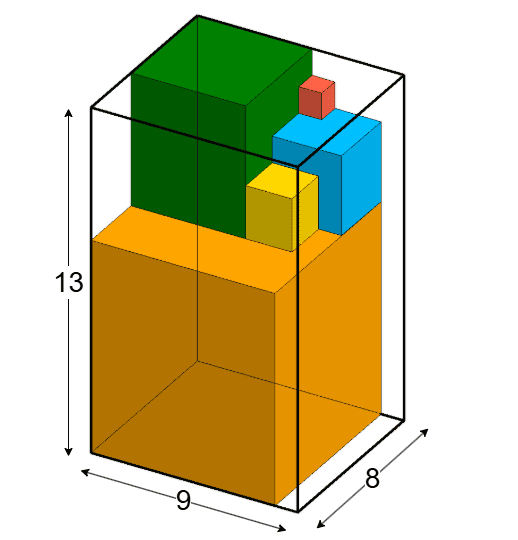
在第一个测试用例中,只有一个盒子是合适的。立方体可以按如下方式放入其中:
翻译由 DeepSeek R1 完成。