CF2111B Fibonacci Cubes

There are $ n $ Fibonacci cubes, where the side of the $ i $-th cube is equal to $ f_{i} $ , where $ f_{i} $ is the $ i $-th Fibonacci number. In this problem, the Fibonacci numbers are defined as follows: - $ f_{1} = 1 $ - $ f_{2} = 2 $ - $ f_{i} = f_{i - 1} + f_{i - 2} $ for $ i > 2 $ There are also $ m $ empty boxes, where the $ i $-th box has a width of $ w_{i} $, a length of $ l_{i} $, and a height of $ h_{i} $. For each of the $ m $ boxes, you need to determine whether all the cubes can fit inside that box. The cubes must be placed in the box following these rules: - The cubes can only be stacked in the box such that the sides of the cubes are parallel to the sides of the box; - Every cube must be placed either on the bottom of the box, or on top of other cubes in such a way that all space below the cube is occupied; - A larger cube cannot be placed on top of a smaller cube.

Each test consists of several test cases. The first line contains a single integer $ t $ ($ 1 \le t \le 10^{3} $) — the number of test cases. The description of the test cases follows. In the first line of each test case, there are two integers $ n $ and $ m $ ($ 2 \le n \le 10, 1 \le m \le 2 \cdot 10^{5} $) — the number of cubes and the number of empty boxes. The next $ m $ lines of each test case contain $ 3 $ integers $ w_{i} $, $ l_{i} $, and $ h_{i} $ ($ 1 \le w_{i}, l_{i}, h_{i} \le 150 $) — the dimensions of the $ i $-th box. Additional constraints on the input: - The sum of $ m $ across all test cases does not exceed $ 2 \cdot 10^{5} $ .

For each test case, output a string of length $ m $ , where the $ i $-th character is equal to "1" if all $ n $ cubes can fit into the $ i $-th box; otherwise, the $ i $-th character is equal to "0".

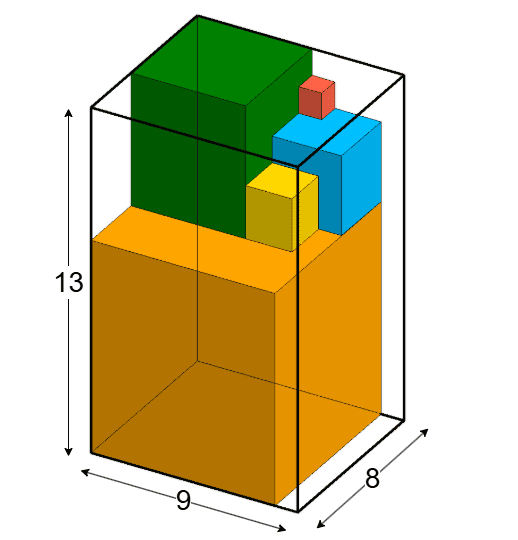
In the first test case, only one box is suitable. The cubes can be placed in it as follows: