CF2111F Puzzle

你收到了一份拼图礼物，每块拼图都是边长为 $1$ 的正方形。你可以在这幅拼图上粘贴任意图片，然后将其切割，得到一副几乎普通的拼图。 你的朋友是一位狂热的数学家，于是他建议你考虑如下问题。是否可以将这些拼图块排列，使得满足以下条件： - 拼图块的边与坐标轴平行； - 拼图块之间不重叠； - 所有拼图块组成一个连通块（即任意两块之间存在一条路径，每一步都经过相邻且共边的拼图块）； - 该连通块的周长与面积之比等于 $ \frac{p}{s} $； - 使用的拼图块数量不超过 $50\,000$。 你能解决这个问题吗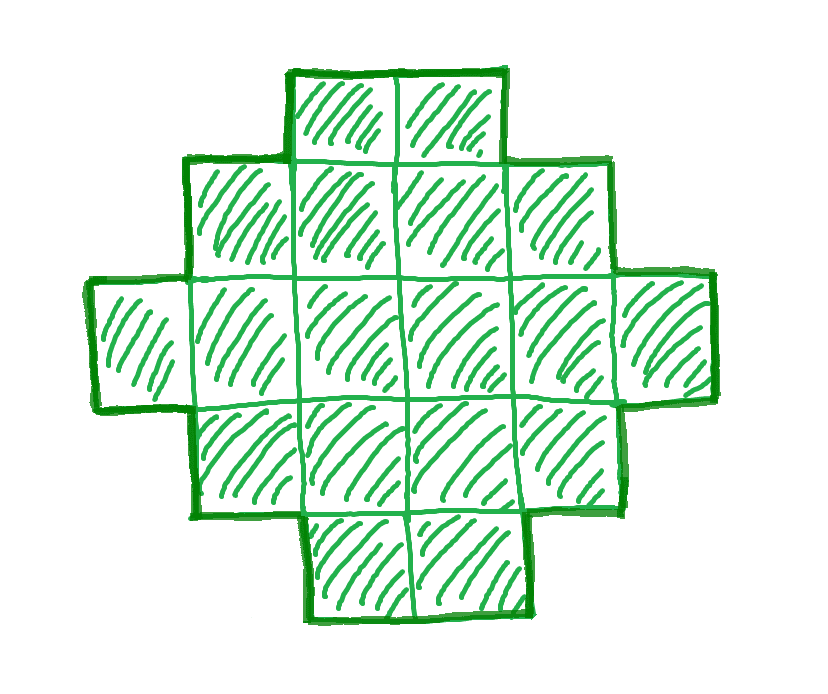？  对于上图，周长与面积之比为 $ \frac{11}{9} $。

每个测试包含若干组数据。第一行包含一个整数 $ t $（$1 \le t \le 10$），表示测试组数。接下来每组数据一行，包含两个整数 $ p $ 和 $ s $（$1 \le p, s \le 50$）。

对于每组测试数据： - 如果无法按照上述要求排列拼图块，输出一行 $-1$； - 否则，第一行输出一个整数 $k$（$1 \le k \le 50\,000$），接下来 $k$ 行，每行两个整数 $x_{i}$ 和 $y_{i}$（$-10^{9} \le x_{i}, y_{i} \le 10^{9}$），表示每块拼图块的坐标。如果存在多种满足条件的拼图方案，输出任意一种即可。

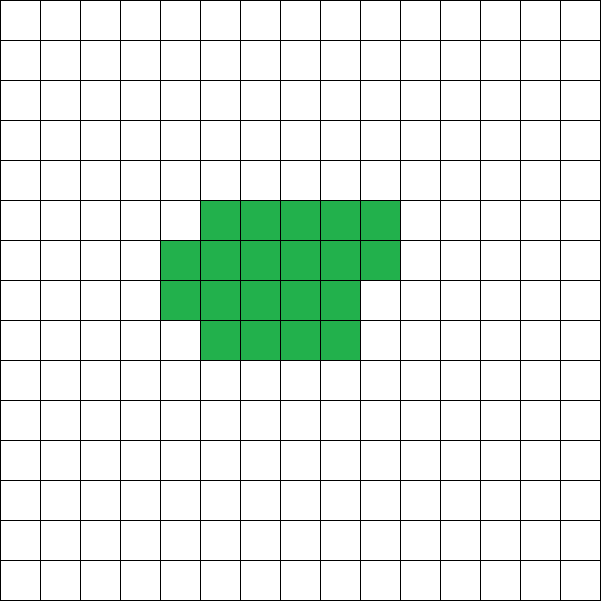
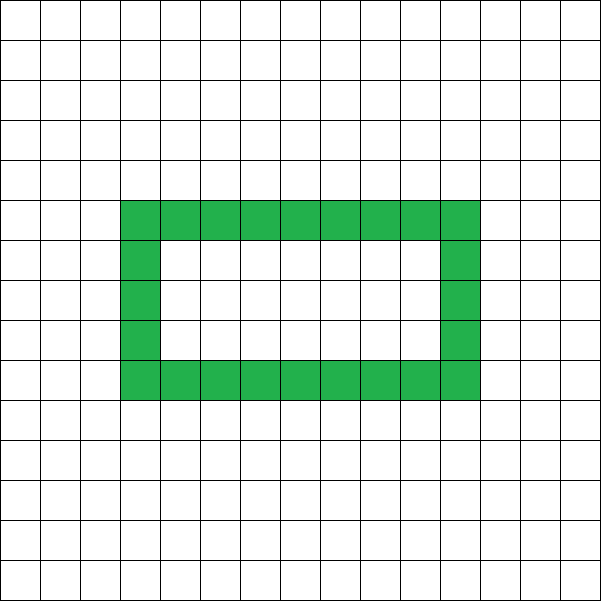
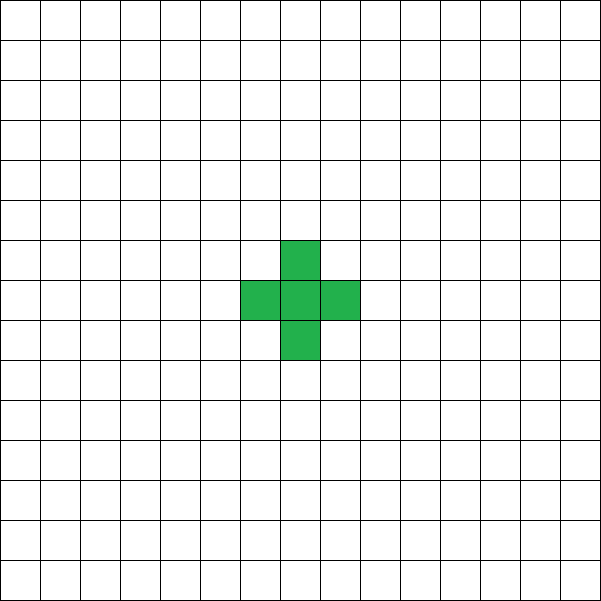
在第一个测试的第一组数据中，图形可能如下所示：  在第二组测试中，图形可能如下：   注意，内部的周长也需要计入！ 由 ChatGPT 4.1 翻译