CF2112D Reachability and Tree
题目描述
考虑一个有向图,我们称有序数对 $(u,v)$ 是好的当且仅当 $u\ne v$ 且图中存在一条 $u$ 到 $v$ 的路径。
给你一棵 $n$ 个结点的树,问有没有一种把这棵树的所有 $n-1$ 条边确定方向的方案,使得形成的有向图中恰有 $n$ 个好的数对。如果存在,给出任意一种方案。
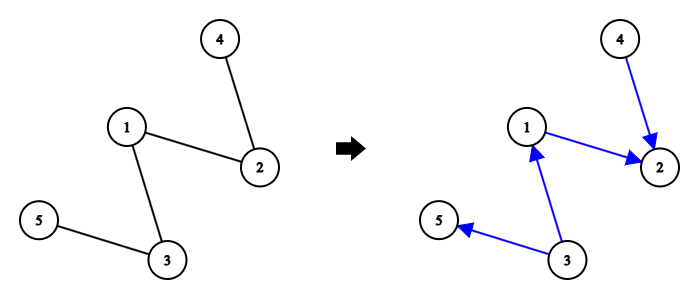
对于第一组数据,这是一种可能的定向方案。
输入格式
多组数据。第一行一个整数 $t(1\le t\le 10^4)$,表示数据组数。
对于每组数据,第一行输入一个正整数 $n(2\le n\le 2\times 10^5)$。
接下来 $n-1$ 行,每行输入两个整 $u_i,v_i(1\le u_i,v_i\le n,u_i\ne v_i)$,表示树上的一条边。
保证每组数据输入的图均构成一棵无向树。保证单个测试点内 $n$ 的和不超过 $2\times 10^5$。
输出格式
对于每组数据,如果不存在定向方案使得形成的有向图中恰有 $n$ 个好的数对,输出一行 `NO`(大小写不敏感)。
否则,输出一行 `YES`(大小写不敏感),接下来输出 $n-1$ 行,每行两个正整数 $u_i,v_i$,表示你给出的方案形成的有向图中一条结点 $u_i$ 指向结点 $v_i$ 的边。边的输出顺序不限。如果有多种解,输出任意一种均可。
说明/提示
**样例解释**
对于第一组数据,一种可能的定向方案如上图所示。在此方案中五个好的数对为 $(3,5),(3,1),(3,2),(1,2),(4,2)$。
对于第二组数据,一种可能的定向方案如下图所示。
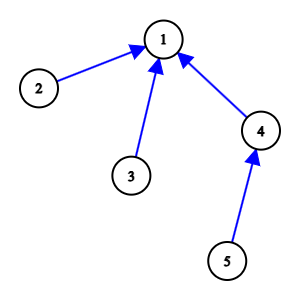
在此方案中五个好的数对为 $(2,1),(3,1),(4,1),(5,4),(5,1)$。
对于第三组数据,只有两个有序数对,无论这条唯一的边指向哪个方向,都只有一个数对会是好的。