CF2112D Reachability and Tree

Let $ u $ and $ v $ be two distinct vertices in a directed graph. Let's call the ordered pair $ (u, v) $ good if there exists a path from vertex $ u $ to vertex $ v $ along the edges of the graph. You are given an undirected tree with $ n $ vertices and $ n - 1 $ edges. Determine whether it is possible to assign a direction to each edge of this tree so that the number of good pairs in it is exactly $ n $ . If it is possible, print any way to direct the edges resulting in exactly $ n $ good pairs. 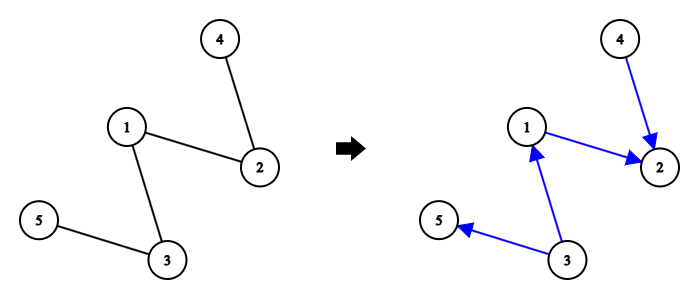 One possible directed version of the tree for the first test case.

The first line contains one integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases. The first line of each test case contains one integer $ n $ ( $ 2 \le n \le 2 \cdot 10^5 $ ) — the number of vertices in the tree. The next $ n - 1 $ lines describe the edges. The $ i $ -th line contains two integers $ u_i $ and $ v_i $ ( $ 1 \le u_i, v_i \le n $ ; $ u_i \neq v_i $ ) — the vertices connected by the $ i $ -th edge. It is guaranteed that the edges in each test case form an undirected tree and that the sum of $ n $ over all test cases does not exceed $ 2 \cdot 10^5 $ .

For each test case, print "NO" (case-insensitive) if it is impossible to direct all edges of the tree and obtain exactly $ n $ good pairs of vertices. Otherwise, print "YES" (case-insensitive) and then print $ n - 1 $ pairs of integers $ u_i $ and $ v_i $ separated by spaces — the edges directed from $ u_i $ to $ v_i $ . The edges can be printed in any order. If there are multiple answers, output any.

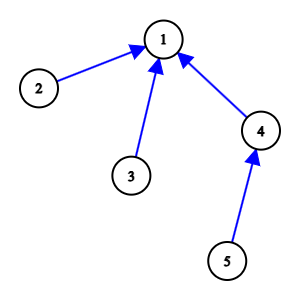The tree from the first test case and its possible directed version are shown in the legend above. In this version, there are exactly $ 5 $ good pairs of vertices: $ (3, 5) $ , $ (3, 1) $ , $ (3, 2) $ , $ (1, 2) $ , and $ (4, 2) $ . One possible directed version of the tree from the second test case is shown below: In the presented answer, there are exactly $ 5 $ good pairs of vertices: $ (2, 1) $ , $ (3, 1) $ , $ (4, 1) $ , $ (5, 4) $ , and $ (5, 1) $ . In the third test case, there are only two directed pairs of vertices, but for any direction of the edge, only one pair will be good.