CF2114D Come a Little Closer

The game field is a matrix of size $ 10^9 \times 10^9 $ , with a cell at the intersection of the $ a $ -th row and the $ b $ -th column denoted as ( $ a, b $ ). There are $ n $ monsters on the game field, with the $ i $ -th monster located in the cell ( $ x_i, y_i $ ), while the other cells are empty. No more than one monster can occupy a single cell. You can move one monster to any cell on the field that is not occupied by another monster at most once . After that, you must select one rectangle on the field; all monsters within the selected rectangle will be destroyed. You must pay $ 1 $ coin for each cell in the selected rectangle. Your task is to find the minimum number of coins required to destroy all the monsters.

The first line contains a single integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases. The first line of each test case contains a single integer $ n $ ( $ 1 \le n \le 2 \cdot 10^5 $ ) — the number of monsters on the field. The following $ n $ lines contain two integers $ x_i $ and $ y_i $ ( $ 1 \le x_i, y_i \le 10^9 $ ) — the coordinates of the cell with the $ i $ -th monster. All pairs ( $ x_i, y_i $ ) are distinct. It is guaranteed that the sum of $ n $ across all test cases does not exceed $ 2 \cdot 10^5 $ .

For each test case, output a single integer — the minimum cost to destroy all $ n $ monsters.

Below are examples of optimal moves, with the cells of the rectangle to be selected highlighted in green. 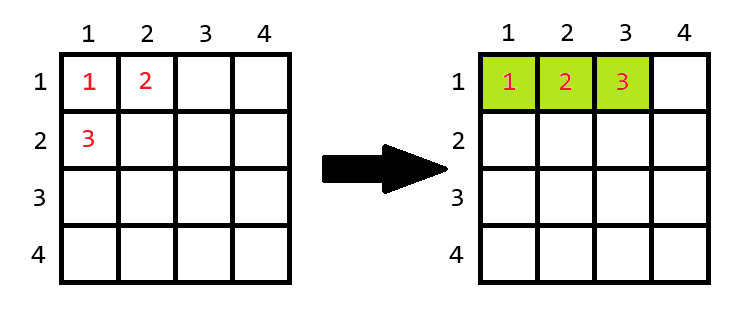 Required move for the first example. 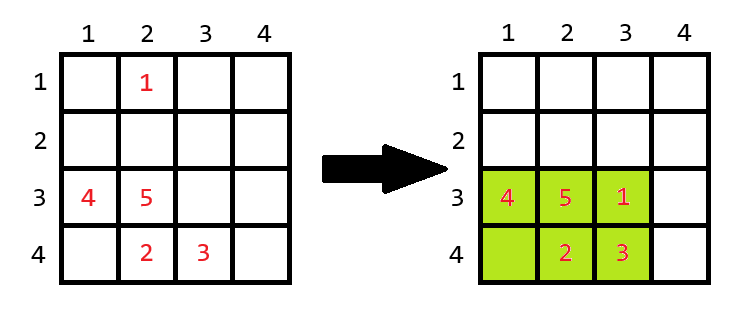 Required move for the fifth example.