CF2117F Wildflower

Yousef has a rooted tree $ ^{\text{∗}} $ consisting of exactly $ n $ vertices, which is rooted at vertex $ 1 $ . You would like to give Yousef an array $ a $ of length $ n $ , where each $ a_i $ $ (1 \le i \le n) $ can either be $ 1 $ or $ 2 $ . Let $ s_u $ denote the sum of $ a_v $ where vertex $ v $ is in the subtree $ ^{\text{†}} $ of vertex $ u $ . Yousef considers the tree special if all the values in $ s $ are pairwise distinct (i.e., all subtree sums are unique). Your task is to help Yousef count the number of different arrays $ a $ that result in the tree being special. Two arrays $ b $ and $ c $ are different if there exists an index $ i $ such that $ b_i \neq c_i $ . As the result can be very large, you should print it modulo $ 10^9 + 7 $ . $ ^{\text{∗}} $ A tree is a connected undirected graph with $ n - 1 $ edges. $ ^{\text{†}} $ The subtree of a vertex $ v $ is the set of all vertices that pass through $ v $ on a simple path to the root. Note that vertex $ v $ is also included in the set.

The first line contains an integer $ t $ $ (1 \le t \le 10^4) $ — the number of test cases. Each test case consists of several lines. The first line of the test case contains an integer $ n $ $ (2 \le n \le 2 \cdot 10^5) $ — the number of vertices in the tree. Then $ n−1 $ lines follow, each of them contains two integers $ u $ and $ v $ $ (1 \le u,v \le n, u \ne v) $ which describe a pair of vertices connected by an edge. It is guaranteed that the given graph is a tree and has no loops or multiple edges. It is guaranteed that the sum of $ n $ over all test cases doesn't exceed $ 2 \cdot 10^5 $ .

For each test case, print one integer $ x $ — the number of different arrays $ a $ that result in the tree being special, modulo $ 10^9 + 7 $ .

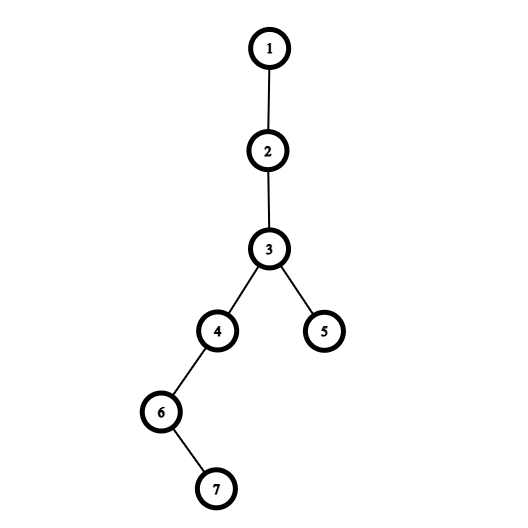
The tree given in the fifth test case: