CF2118E Grid Coloring

有一个 $n \times m$ 的网格，初始时每个格子都是白色的。你需要依次为所有格子染色。每当你染色一个格子时，所有距离它最远的已染色格子会受到一次惩罚。请你给出一种染色顺序，使得没有任何格子的惩罚次数超过 $3$。 注意，$n$ 和 $m$ 都是奇数。 本题使用的距离度量为“棋盘距离”（[Chebyshev 距离](https://en.wikipedia.org/wiki/Chebyshev_distance)），在判定距离相等时，使用“曼哈顿距离”（[Taxicab 距离](https://en.wikipedia.org/wiki/Taxicab_geometry#Formal_definition)）来决定优先级。具体来说，若有格子 $(x_2, y_2)$ 和 $(x_3, y_3)$，对于格子 $(x_1, y_1)$，如果满足下列条件之一，则认为 $(x_2, y_2)$ 比 $(x_3, y_3)$ 更远： - $\max\big(\lvert x_1 - x_2 \rvert, \lvert y_1 - y_2 \rvert\big) > \max\big(\lvert x_1 - x_3 \rvert, \lvert y_1 - y_3 \rvert\big)$ - $\max\big(\lvert x_1 - x_2 \rvert, \lvert y_1 - y_2 \rvert\big) = \max\big(\lvert x_1 - x_3 \rvert, \lvert y_1 - y_3 \rvert\big)$ 且 $\lvert x_1 - x_2 \rvert + \lvert y_1 - y_2 \rvert > \lvert x_1 - x_3 \rvert + \lvert y_1 - y_3 \rvert$ 可以证明，至少存在一种可行解。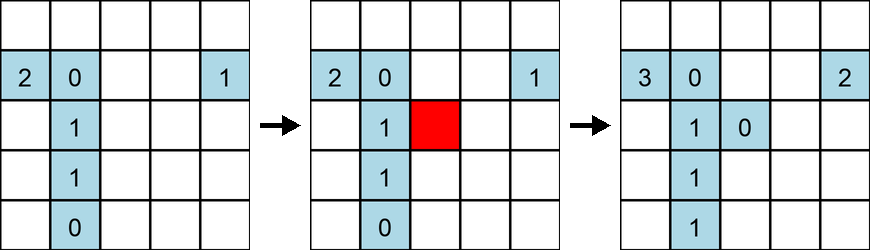  上图展示了在 $5 \times 5$ 网格中染色中心格子后各格子的惩罚变化。数字表示各格子的惩罚次数。

每组测试数据包含多个测试用例。第一行包含一个整数 $t$（$1 \le t \le 100$），表示测试用例的数量。 每个测试用例的第一行包含两个奇数整数 $n$ 和 $m$（$1 \le n, m \le 4999$），分别表示行数和列数。 保证所有测试用例中 $n \cdot m$ 的总和不超过 $5000$。

对于每个测试用例，输出 $n \cdot m$ 行，第 $i$ 行输出你选择的第 $i$ 个染色格子的坐标。若有多种方案，输出任意一种均可。 样例输出中的空行仅为增强可读性，你不需要输出空行。

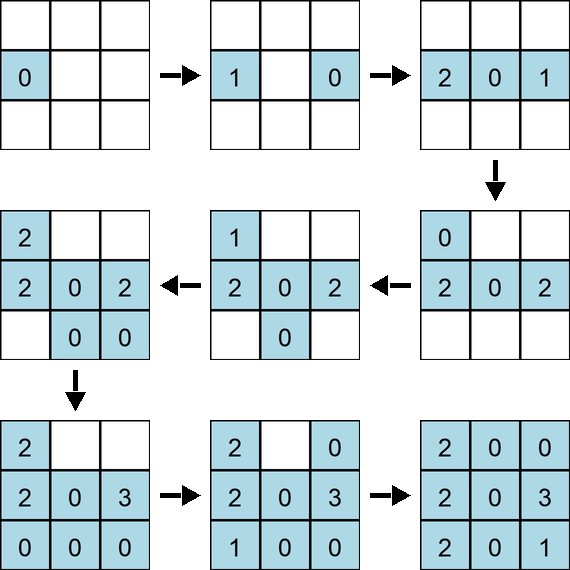
在第一个测试用例中，网格可以按如下方式染色：  数字表示各格子的惩罚次数。 由 ChatGPT 4.1 翻译