CF2119B Line Segments

[PIKASONIC - Lost My Mind (feat.nakotanmaru)](https://www.youtube.com/watch?v=iprl3wJnWoo) You are given two points $ (p_x,p_y) $ and $ (q_x,q_y) $ on a Euclidean plane. You start at the starting point $ (p_x,p_y) $ and will perform $ n $ operations. In the $ i $ -th operation, you must choose any point such that the Euclidean distance $ ^{\text{∗}} $ between your current position and the point is exactly $ a_i $ , and then move to that point. Determine whether it is possible to reach the terminal point $ (q_x,q_y) $ after performing all operations. $ ^{\text{∗}} $ The Euclidean distance between $ (x_1, y_1) $ and $ (x_2, y_2) $ is $ \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 10^4 $ ). The description of the test cases follows. The first line of each test case contains a single integer $ n $ ( $ 1\leq n \leq 10^3 $ ) — the length of the sequence $ a $ . The second line of each test case contains four integers $ p_x,p_y,q_x,q_y $ ( $ 1\leq p_x,p_y,q_x,q_y\leq 10^7 $ ) — the coordinates of the starting point and terminal point. The third line of each test case contains $ n $ integers $ a_1,a_2,\ldots,a_n $ ( $ 1 \le a_i \le 10^4 $ ) — the distance to move in each operation. It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 2\cdot 10^5 $ .

For each test case, output "Yes" if it is possible to reach the terminal point $ (q_x,q_y) $ after all operations; otherwise, output "No". You can output the answer in any case (upper or lower). For example, the strings "yEs", "yes", "Yes", and "YES" will be recognized as positive responses.

Here is a picture that shows a possible movement of the first test case. The coordinates of point $ r_1 $ are $ (3,1+\sqrt{5}) $ . 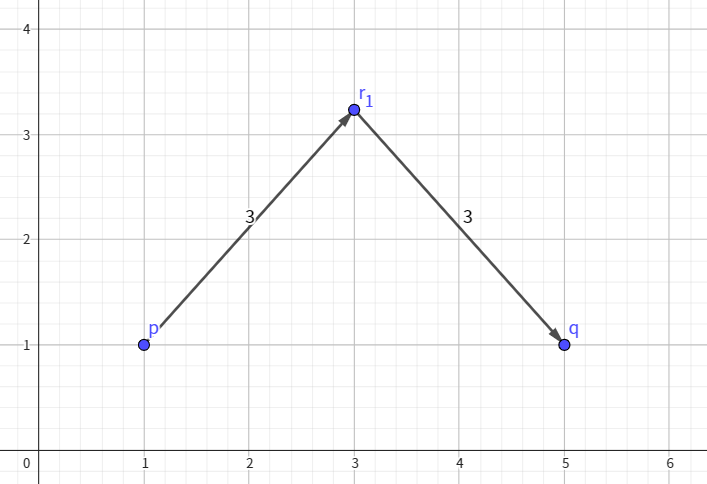 The first test case.Here is a picture that shows a possible movement of the second test case. The coordinates of point $ r_1 $ are $ (1+\sqrt{3},0) $ , and the coordinates of point $ r_2 $ are $ \left(-\frac{(\sqrt{3}+4)(3\sqrt{3(149-24\sqrt{3})}-7\sqrt{3}-38)}{104},-\frac{\sqrt{3(1331-764\sqrt{3})}+12\sqrt{3}-27}{104}\right) $ . 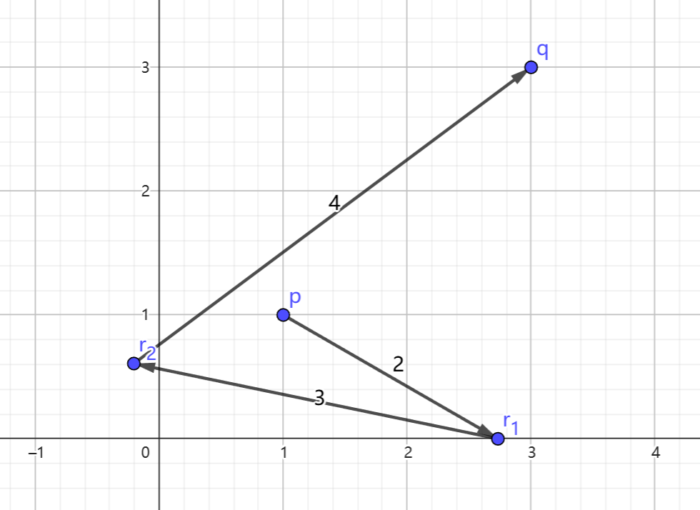 The second test case.For the third test case, it can be shown that there is no set of moves that satisfies all requirements. Here is a picture that shows a possible movement of the fourth test case. 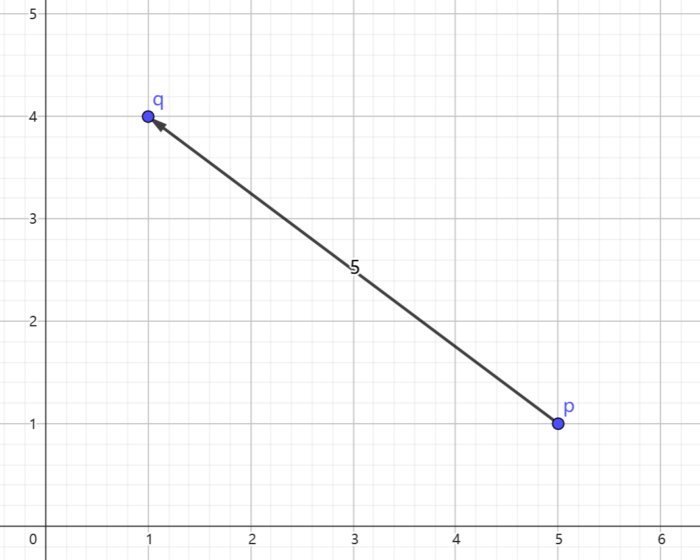 The fourth test case.