CF2119B Line Segments

[PIKASONIC - Lost My Mind (feat.nakotanmaru)](https://www.youtube.com/watch?v=iprl3wJnWoo) 在一个欧几里得平面上，你被给予两个点：起点 $(p_x, p_y)$ 和终点 $(q_x, q_y)$。你的任务是从起点出发，执行 $n$ 次操作，每次操作必须选择一个点，使得当前位置到该点的欧几里得距离恰好为 $a_i$，然后移动到该点。判断是否可以在执行完所有操作后到达终点 $(q_x, q_y)$。

- 第一行包含测试用例的数量 $t$（$1 \le t \le 10^4$）。 - 每个测试用例的第一行包含一个整数 $n$（$1 \le n \le 10^3$），表示操作次数。 - 第二行包含四个整数 $p_x, p_y, q_x, q_y$（$1 \le p_x, p_y, q_x, q_y \le 10^7$），表示起点和终点的坐标。 - 第三行包含 $n$ 个整数 $a_1, a_2, \ldots, a_n$（$1 \le a_i \le 10^4$），表示每次操作必须移动的距离。

对于每个测试用例，如果可以在执行完所有操作后到达终点，输出 `Yes`（大小写不限）；否则输出 `No`。

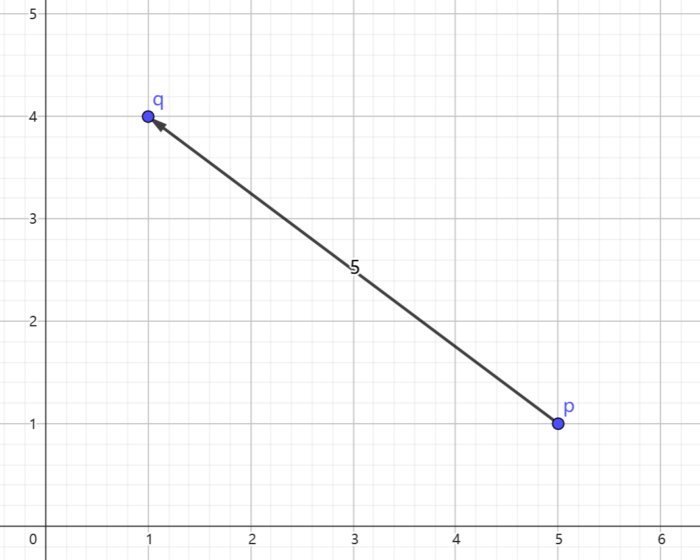
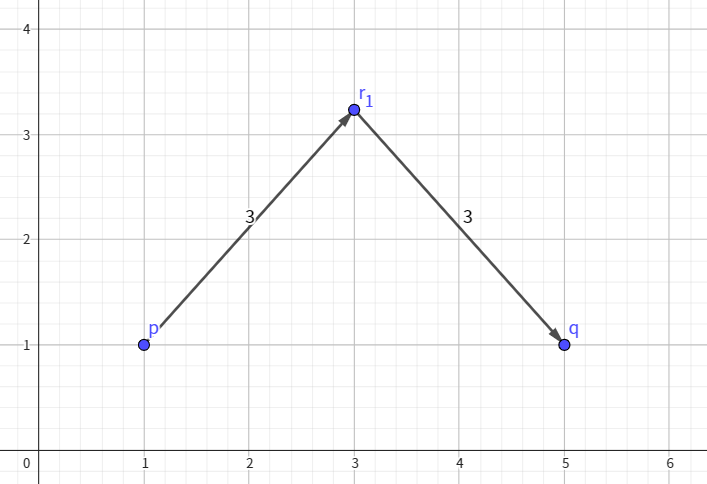
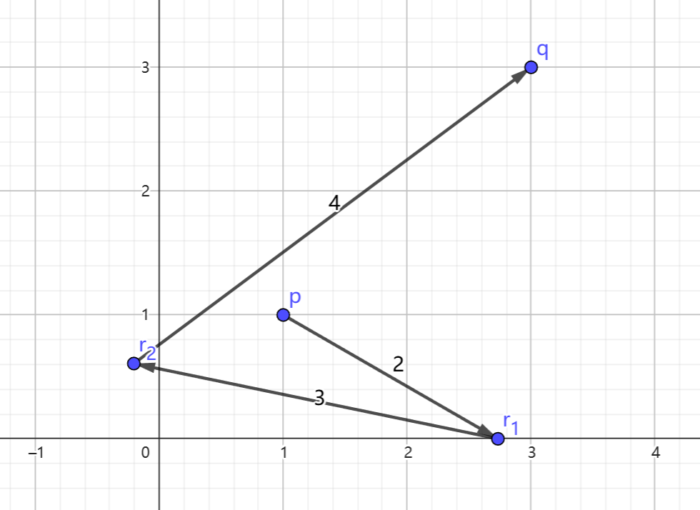
- 欧几里得距离公式：点 $(x_1, y_1)$ 和 $(x_2, y_2)$ 之间的距离为 $\sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}$。 这是一张展示第一个测试用例可能移动路径的示意图。点 $ r_1 $ 的坐标为 $ (3,1+\sqrt{5}) $ 。  这是一张展示第二个测试用例可能移动路径的示意图。 点 $ r_1 $ 的坐标为 $ (1+\sqrt{3},0) $，点 $ r_2 $ 的坐标为 $ \left(-\frac{(\sqrt{3}+4)(3\sqrt{3(149-24\sqrt{3})}-7\sqrt{3}-38)}{104},-\frac{\sqrt{3(1331-764\sqrt{3})}+12\sqrt{3}-27}{104}\right) $ 。  对于第三个测试用例，可以证明不存在满足所有要求的移动方案。 这是一张展示第四个测试用例可能移动路径的示意图。