CF2120D Matrix game

Aryan and Harshith play a game. They both start with three integers $ a $ , $ b $ , and $ k $ . Aryan then gives Harshith two integers $ n $ and $ m $ . Harshith then gives Aryan a matrix $ X $ with $ n $ rows and $ m $ columns, such that each of the elements of $ X $ is between $ 1 $ and $ k $ (inclusive). After that, Aryan wins if he can find a submatrix $ ^{\text{∗}} $ $ Y $ of $ X $ with $ a $ rows and $ b $ columns such that all elements of $ Y $ are equal. For example, when $ a=2, b=2, k=6, n=3 $ and $ m=3 $ , if Harshith gives Aryan the matrix below, it is a win for Aryan as it has a submatrix of size $ 2\times 2 $ with all elements equal to $ 1 $ as shown below. 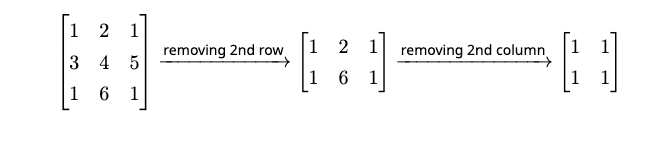 Example of a matrix where Aryan wins Aryan gives you the values of $ a $ , $ b $ , and $ k $ . He asks you to find the lexicographically minimum tuple $ (n,m) $ that he should give to Harshith such that Aryan always wins. Help Aryan win the game. Assume that Harshith plays optimally. The values of $ n $ and $ m $ can be large, so output them modulo $ 10^9+7 $ . A tuple $ (n_1, m_1) $ is said to be lexicographically smaller than $ (n_2, m_2) $ if either $ n_1

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 10^4 $ ). The description of the test cases follows. Each test case contains a single line with three space-separated integers $ a, b $ and $ k $ ( $ 1\leq a,b,k\leq 10^5 $ ). It is guaranteed that the sum of $ \max(a, b, k) $ over all test cases does not exceed $ 10^5 $ .

For each test case, output a single line containing two space-separated integers $ n $ and $ m $ , denoting the answer to the problem. The values of $ n $ and $ m $ can be large, so output them modulo $ 10^9+7 $ .

For the first test case, every $ n\times m $ matrix contains a $ 1\times 1 $ submatrix with all elements equal. $ (1,1) $ is the lexicographically minimum tuple among all of them. For the second test case, it can be verified that whatever $ 3\times 7 $ matrix Harshith gives to Aryan, Aryan can always win by finding a $ 2\times 2 $ submatrix with all elements equal. $ (3,7) $ is also the lexicographically minimum tuple among all possible tuples where Aryan always wins.