CF2120F Superb Graphs

众所周知，Aryan 是个有趣的人。他决定创造一些有趣的图。对于一个图 $G$，他如下定义 $G$ 的有趣图 $G'$： - $G'$ 中的每个顶点 $v'$ 对应 $G$ 中的一个非空独立集$^{\text{∗}}$或团$^{\text{†}}$。 - $G'$ 中所有顶点对应的 $G$ 中顶点集合两两不交，且并集覆盖 $G$ 的所有顶点。换言之，$G'$ 中顶点对应的 $G$ 中顶点集合构成了 $G$ 的顶点集的一个划分。 - 如果在 $G'$ 中，一条边连接了两个顶点 $v_1'$ 和 $v_2'$，那么在 $G$ 中，$v_1'$ 对应的集合中的每个顶点都与 $v_2'$ 对应的集合中的每个顶点有一条边相连。 - 如果在 $G'$ 中，两个顶点 $v_1'$ 和 $v_2'$ 之间没有边，那么在 $G$ 中，$v_1'$ 对应的集合中的任意顶点与 $v_2'$ 对应的集合中的任意顶点之间都没有边相连。 又一次众所周知，Harshith 是个绝妙的人。他决定使用有趣的图来创造他自己的绝妙图。对于一个图 $G$，一个有趣的图 $G''$ 如果在其所有可能的有趣图中顶点数最少，则被称为 $G$ 的绝妙图。 Aryan 给了 Harshith $k$ 个简单无向图$^{\text{‡}}$ $G_1, G_2, \ldots, G_k$，它们都建立在同一个顶点集 $V$ 上。Harshith 想知道，是否存在另外 $k$ 个图 $H_1, H_2, \ldots, H_k$，它们都建立在某个另一个顶点集 $V'$ 上，满足以下条件： - 对于所有的 $i \in \{1, 2, \ldots, k\}$，$G_i$ 是 $H_i$ 的绝妙图。 - 如果在某对 $(G_i, H_i)$ 中（$1 \le i \le k$），顶点 $v \in V$ 对应于 $H_i$ 中一个大小大于 1 的独立集，那么在任何其他对 $(G_j, H_j)$ 中（$1 \le j \le k, j \neq i$），$v$ 不能对应于 $H_j$ 中一个大小大于 1 的团。 请帮助 Harshith 解决他的疑问。 $^{\text{∗}}$ 对于一个图 $G$，如果一个顶点子集 $S$ 中任意两个顶点之间都没有边相连，则称 $S$ 为一个独立集。 $^{\text{†}}$ 对于一个图 $G$，如果一个顶点子集 $S$ 中的每个顶点都与 $S$ 中所有其他顶点有边相连，则称 $S$ 为一个团。 $^{\text{‡}}$ 如果一个图的边是无向的，且没有自环或重边，则称其为简单无向图。

每个测试文件包含多组测试用例。第一行包含一个整数 $t$（$1 \le t \le 100$），表示测试用例的数量。接下来是各组测试用例的描述。 每个测试用例的第一行包含两个整数 $n$ 和 $k$（$1 \le n \le 300, 1 \le k \le 10$）。 接下来是 $k$ 个图的描述。每个图的描述的第一行包含一个整数 $m$（$0 \le m \le \frac{n \cdot (n-1)}{2}$）。 接下来的 $m$ 行，每行包含两个以空格分隔的整数 $u$ 和 $v$（$1 \le u, v \le n, u \neq v$），表示顶点 $u$ 和 $v$ 之间有一条边。 保证所有测试用例中所有图的 $m$ 之和不超过 $2 \cdot 10^5$，所有测试用例的 $n$ 之和不超过 $300$。

对于每个测试用例，如果存在满足条件的 $k$ 个图，则输出 "Yes"；否则输出 "No"。 你可以以任何大小写形式输出答案。例如，字符串 "yEs"、"yes"、"Yes" 和 "YES" 都将被视作肯定的回答。

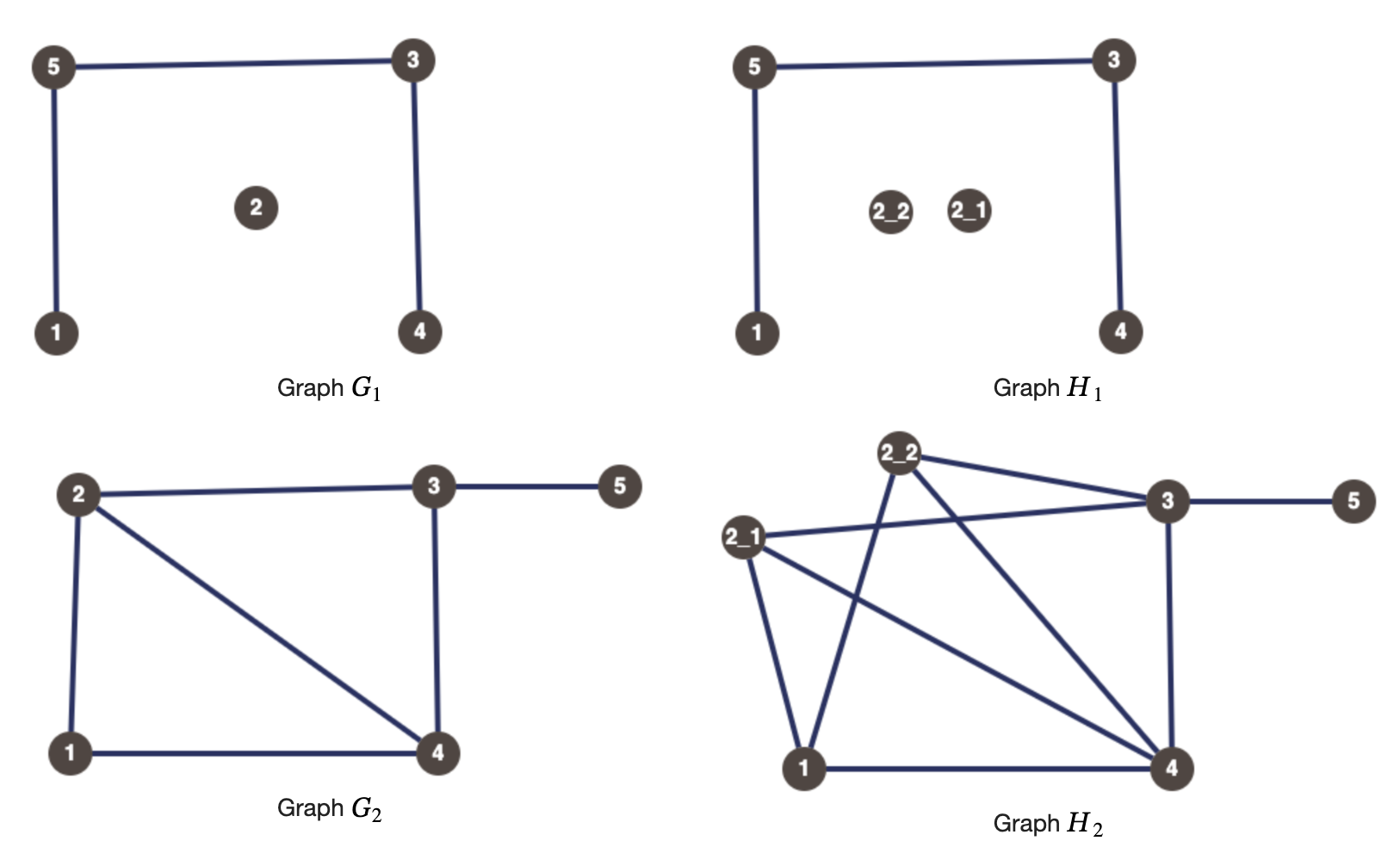
对于第一个测试用例，下面给出了图 $G_1, H_1$ 和 $G_2, H_2$ 的示例，使得 $G_1$ 是 $H_1$ 的绝妙图，$G_2$ 是 $H_2$ 的绝妙图。  在每对图中，$G_i$ 的顶点 2 对应于相应 $H_i$ 的独立集 $\{2\_1, 2\_2\}$，而 $G_i$ 的其余顶点 $v \in \{1, 3, 4, 5\}$ 对应于相应 $H_i$ 中的独立集/团 $\{v\}$（单个顶点的集合既可以被看作是独立集，也可以被看作是团）。 对于第三个测试用例，可以证明答案是 "No"。 使用 Gemini 2.5pro 翻译。