CF2120F Superb Graphs

As we all know, Aryan is a funny guy. He decides to create fun graphs. For a graph $ G $ , he defines fun graph $ G' $ of $ G $ as follows: - Every vertex $ v' $ of $ G' $ maps to a non-empty independent set $ ^{\text{∗}} $ or clique $ ^{\text{†}} $ in $ G $ . - The sets of vertices of $ G $ that the vertices of $ G' $ map to are pairwise disjoint and combined cover all the vertices of $ G $ , i.e., the sets of vertices of $ G $ mapped by vertices of $ G' $ form a partition of the vertex set of $ G $ . - If an edge connects two vertices $ v_1' $ and $ v_2' $ in $ G' $ , then there is an edge between every vertex of $ G $ in the set mapped to $ v_1' $ and every vertex of $ G $ in the set mapped to $ v_2' $ . - If an edge does not connect two vertices $ v_1' $ and $ v_2' $ in $ G' $ , then there is not an edge between any vertex of $ G $ in the set mapped to $ v_1' $ and any vertex of $ G $ in the set mapped to $ v_2' $ . As we all know again, Harshith is a superb guy. He decides to use fun graphs to create his own superb graphs. For a graph $ G $ , a fun graph $ G' ' $ is called a superb graph of $ G $ if $ G' ' $ has the minimum number of vertices among all possible fun graphs of $ G $ . Aryan gives Harshith $ k $ simple undirected graphs $ ^{\text{‡}} $ $ G_1, G_2,\ldots,G_k $ , all on the same vertex set $ V $ . Harshith then wonders if there exist $ k $ other graphs $ H_1, H_2,\ldots,H_k $ , all on some other vertex set $ V' $ such that: - $ G_i $ is a superb graph of $ H_i $ for all $ i\in \{1,2,\ldots,k\} $ . - If a vertex $ v\in V $ maps to an independent set of size greater than $ 1 $ in one $ G_i, H_i $ ( $ 1\leq i\leq k $ ) pair, then there exists no pair $ G_j, H_j $ ( $ 1\leq j\leq k, j\neq i $ ) where $ v $ maps to a clique of size greater than $ 1 $ . Help Harshith solve his wonder. $ ^{\text{∗}} $ For a graph $ G $ , a subset $ S $ of vertices is called an independent set if no two vertices of $ S $ are connected with an edge. $ ^{\text{†}} $ For a graph $ G $ , a subset $ S $ of vertices is called a clique if every vertex of $ S $ is connected to every other vertex of $ S $ with an edge. $ ^{\text{‡}} $ A graph is a simple undirected graph if its edges are undirected and there are no self-loops or multiple edges between the same pair of vertices.

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 100 $ ). The description of the test cases follows. The first line of each test case contains two integers $ n $ and $ k $ ( $ 1\leq n\leq 300, 1\leq k\leq 10 $ ). Then, there are $ k $ graphs described. The first line of each graph description contains a single integer $ m $ ( $ 0\leq m\leq \frac{n\cdot(n-1)}{2} $ ). Next $ m $ lines each contain two space-separated integers $ u $ and $ v $ ( $ 1\leq u, v\leq n, u\neq v $ ), denoting that an edge connects vertices $ u $ and $ v $ . It is guaranteed that the sum of $ m $ over all graphs over all test cases does not exceed $ 2\cdot 10^5 $ , and the sum of $ n $ over all test cases does not exceed $ 300 $ .

For each testcase, print "Yes" if there exists $ k $ graphs satisfying the conditions; otherwise, "No". You can output the answer in any case (upper or lower). For example, the strings "yEs", "yes", "Yes", and "YES" will be recognized as positive responses.

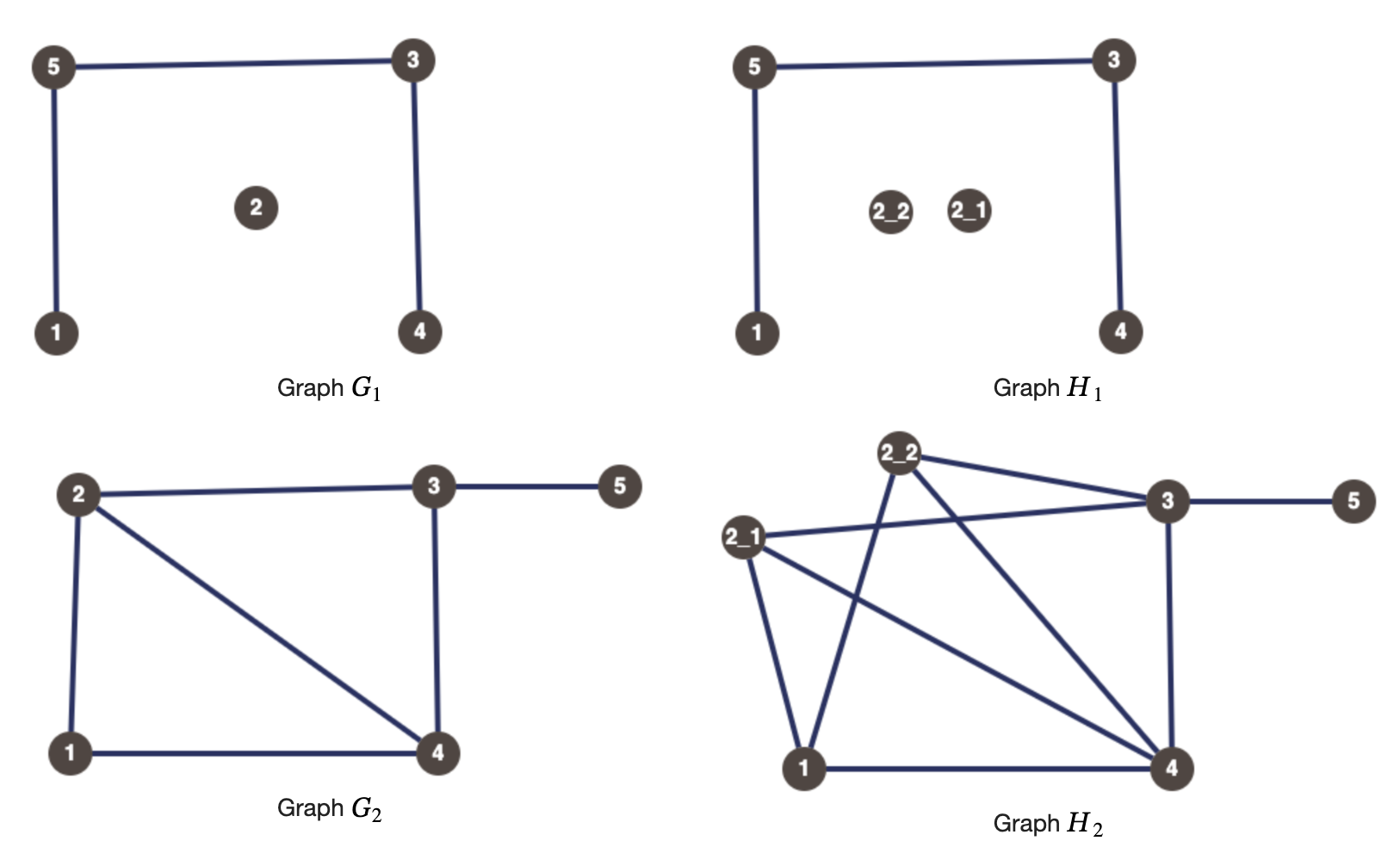For the first test case, the following are the graphs of $ G_1, H_1 $ and $ G_2, H_2 $ such that $ G_1 $ is superb graph of $ H_1 $ and $ G_2 $ is superb graph of $ H_2 $ . In each graph, vertex $ 2 $ of $ G_i $ corresonds to independent set $ \{2\_1, 2\_2\} $ of corresponding $ H_i $ and remaining vertices $ v\in\{1,3,4,5\} $ of $ G_i $ correspond to independent set/clique $ \{v\} $ in corresponding $ H_i $ (a single vertex set can be considered both an independent set and a clique). In the third test case, it can be proven that the answer is "No".