CF2120G Eulerian Line Graph

Aryan loves graph theory more than anything. Well, no, he likes to flex his research paper on line graphs to everyone more. To start a conversation with you, he decides to give you a problem on line graphs. In the mathematical discipline of graph theory, the line graph of a simple undirected graph $ G $ is another simple undirected graph $ L(G) $ that represents the adjacency between every two edges in $ G $ . Precisely speaking, for an undirected graph $ G $ without self-loops or multiple edges, its line graph $ L(G) $ is a graph such that - Each vertex of $ L(G) $ represents an edge of $ G $ . - Two vertices of $ L(G) $ are adjacent if and only if their corresponding edges share a common endpoint in $ G $ . 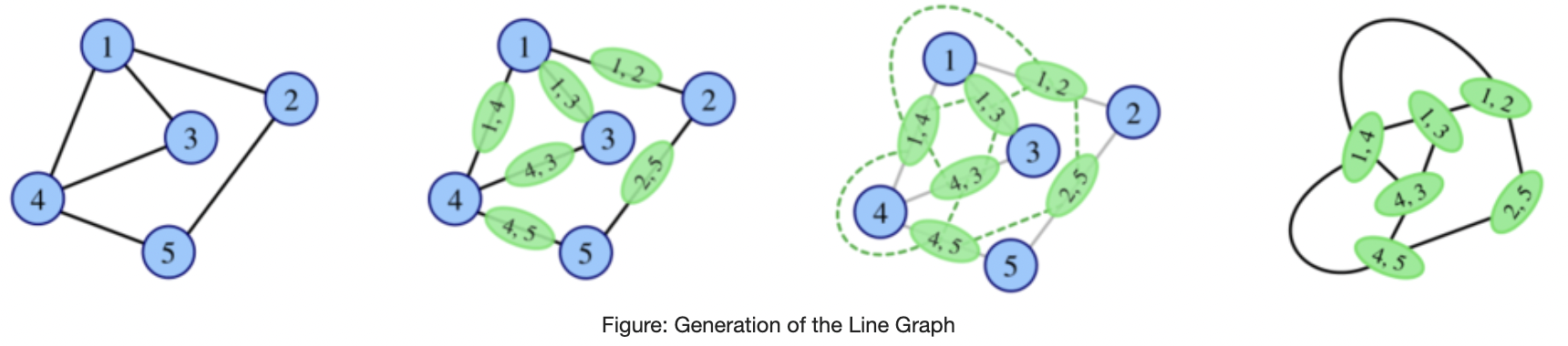Also, $ L^0(G)=G $ and $ L^k(G)=L(L^{k-1}(G)) $ for $ k\geq 1 $ . An Euler trail is a sequence of edges that visits every edge of the graph exactly once. This trail can be either a path (starting and ending at different vertices) or a cycle (starting and ending at the same vertex). Vertices may be revisited during the trail, but each edge must be used exactly once. Aryan gives you a simple connected graph $ G $ with $ n $ vertices and $ m $ edges and an integer $ k $ , and it is guaranteed that $ G $ has an Euler trail and it is not a path graph $ ^{\text{∗}} $ . He asks you to determine if $ L^k(G) $ has an Euler trail. $ ^{\text{∗}} $ A path graph is a tree where every vertex is connected to atmost two other vertices.

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 10^4 $ ). The description of the test cases follows. The first line of each test case contains three space-separated integers $ n $ , $ m $ , and $ k $ ( $ 5 \le n \le 2 \cdot 10^5 $ , $ n-1 \le m \le \min(\frac{n\cdot(n-1)}{2} ,2 \cdot 10^5) $ , $ 1 \le k \le 2 \cdot 10^5 $ ). The next $ m $ lines of each test case contain two space-separated integers $ u $ and $ v $ ( $ 1 \le u,v \le n $ , $ u \neq v $ ), denoting that an edge connects vertices $ u $ and $ v $ . It is guaranteed that the sum of $ n $ and $ m $ over all test cases does not exceed $ 2\cdot 10^5 $ .

For each testcase, print "YES" if $ L^k(G) $ has an Euler trail; otherwise, "NO". You can output the answer in any case (upper or lower). For example, the strings "yEs", "yes", "Yes", and "YES" will be recognized as positive responses.

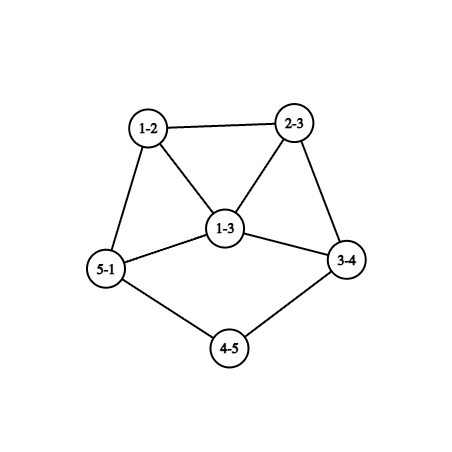
For the first test case, $ L^2(G) $ is isomorphic to $ G $ itself. So, since $ G $ has an Euler trail, $ L^2(G) $ also has an Euler trail. For the second test case, $ L(G) $ looks as follows(Vertex $ i-j $ of $ L(G) $ in figure corresponds to edge between vertices $ i $ and $ j $ of $ G $ ). It can be proven that this doesn't have an Euler trail.