CF2120G Eulerian Line Graph

Aryan 比任何人都热爱图论。其实不然，他更喜欢向所有人炫耀他关于线图的论文。为了和你搭话，他决定给你出一道关于线图的问题。在图论中，一个简单无向图 $G$ 的线图 $L(G)$ 是另一个简单无向图，它表示 $G$ 中每两条边之间的邻接关系。 具体来说，对于一个没有自环和重边的无向图 $G$，其线图 $L(G)$ 满足： - $L(G)$ 的每个顶点对应 $G$ 的一条边。 - 当且仅当 $G$ 中对应的两条边有公共端点时，$L(G)$ 中对应的两个顶点相邻。 此外，$L^0(G)=G$，$L^k(G)=L(L^{k-1}(G))$，其中 $k\geq 1$。 欧拉迹（Euler trail）是一条经过图中每一条边恰好一次的边序列。该轨迹可以是路径（起点和终点不同）或回路（起点和终点相同）。在轨迹过程中，顶点可以重复经过，但每条边必须恰好经过一次。 Aryan 给你一个有 $n$ 个顶点、$m$ 条边的简单连通图 $G$ 和一个整数 $k$，保证 $G$ 存在欧拉迹，且 $G$ 不是路径图$^{\text{∗}}$。他要求你判断 $L^k(G)$ 是否存在欧拉迹。 $^{\text{∗}}$ 路径图是指每个顶点最多与另外两个顶点相连的树。

每组测试数据包含多个测试用例。第一行包含测试用例数 $t$（$1 \le t \le 10^4$）。接下来是每个测试用例的描述。 每个测试用例的第一行包含三个用空格分隔的整数 $n$、$m$ 和 $k$（$5 \le n \le 2 \cdot 10^5$，$n-1 \le m \le \min(\frac{n\cdot(n-1)}{2}, 2 \cdot 10^5)$，$1 \le k \le 2 \cdot 10^5$）。 接下来的 $m$ 行，每行包含两个用空格分隔的整数 $u$ 和 $v$（$1 \le u,v \le n$，$u \neq v$），表示有一条边连接顶点 $u$ 和 $v$。 保证所有测试用例中 $n$ 和 $m$ 的总和不超过 $2\cdot 10^5$。

对于每个测试用例，如果 $L^k(G)$ 存在欧拉迹，输出 "YES"；否则输出 "NO"。 输出不区分大小写。例如，"yEs"、"yes"、"Yes" 和 "YES" 都会被识别为肯定回答。

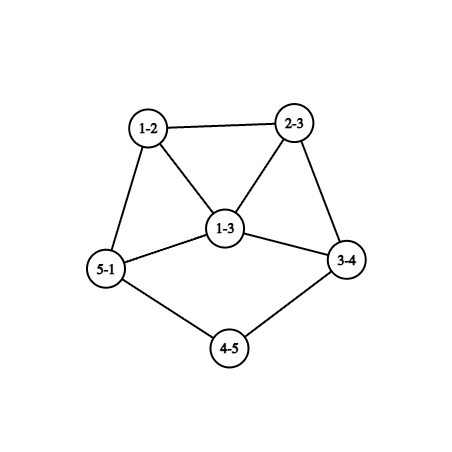
对于第一个测试用例，$L^2(G)$ 与 $G$ 同构。因此，既然 $G$ 存在欧拉迹，$L^2(G)$ 也存在欧拉迹。 对于第二个测试用例，$L(G)$ 如下图所示（图中 $L(G)$ 的顶点 $i-j$ 对应 $G$ 中连接顶点 $i$ 和 $j$ 的边）。可以证明该图不存在欧拉迹。  由 ChatGPT 4.1 翻译