CF2121C Those Who Are With Us

You are given a matrix of integers with $ n $ rows and $ m $ columns. The cell at the intersection of the $ i $ -th row and the $ j $ -th column contains the number $ a_{ij} $ . You can perform the following operation exactly once: - Choose two numbers $ 1 \leq r \leq n $ and $ 1 \leq c \leq m $ . - For all cells $ (i, j) $ in the matrix such that $ i = r $ or $ j = c $ , decrease $ a_{ij} $ by one. You need to find the minimal possible maximum value in the matrix $ a $ after performing exactly one such operation.

Each test consists of multiple test cases. The first line contains a single integer $ t $ ( $ 1 \leq t \leq 10^4 $ ) — the number of test cases. The description of the test cases follows. The first line of each test case contains two integers $ n $ and $ m $ ( $ 1 \leq n \cdot m \leq 10^5 $ ) — the number of rows and columns in the matrix. The next $ n $ lines of each test case describe the matrix $ a $ . The $ i $ -th line contains $ m $ integers $ a_{i1}, a_{i2}, \ldots, a_{im} $ ( $ 1 \leq a_{ij} \leq 100 $ ) — the elements in the $ i $ -th row of the matrix. It is guaranteed that the sum of $ n \cdot m $ across all test cases does not exceed $ 2 \cdot 10^5 $ .

For each test case, output the minimum maximum value in the matrix $ a $ after performing exactly one operation.

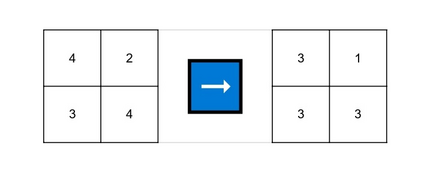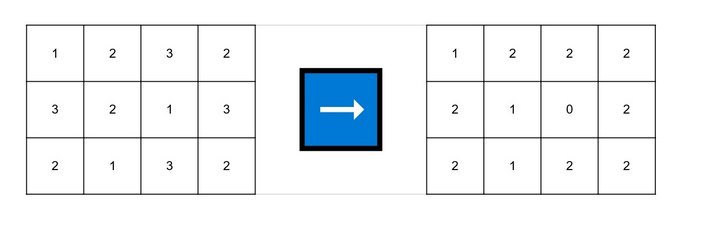In the first three test cases, you can choose $ r = 1 $ and $ c = 1 $ . In the fourth test case, you can choose $ r = 1 $ and $ c = 2 $ . In the fifth test case, you can choose $ r = 2 $ and $ c = 3 $ . In the sixth test case, you can choose $ r = 3 $ and $ c = 2 $ .