CF2122B Pile Shuffling

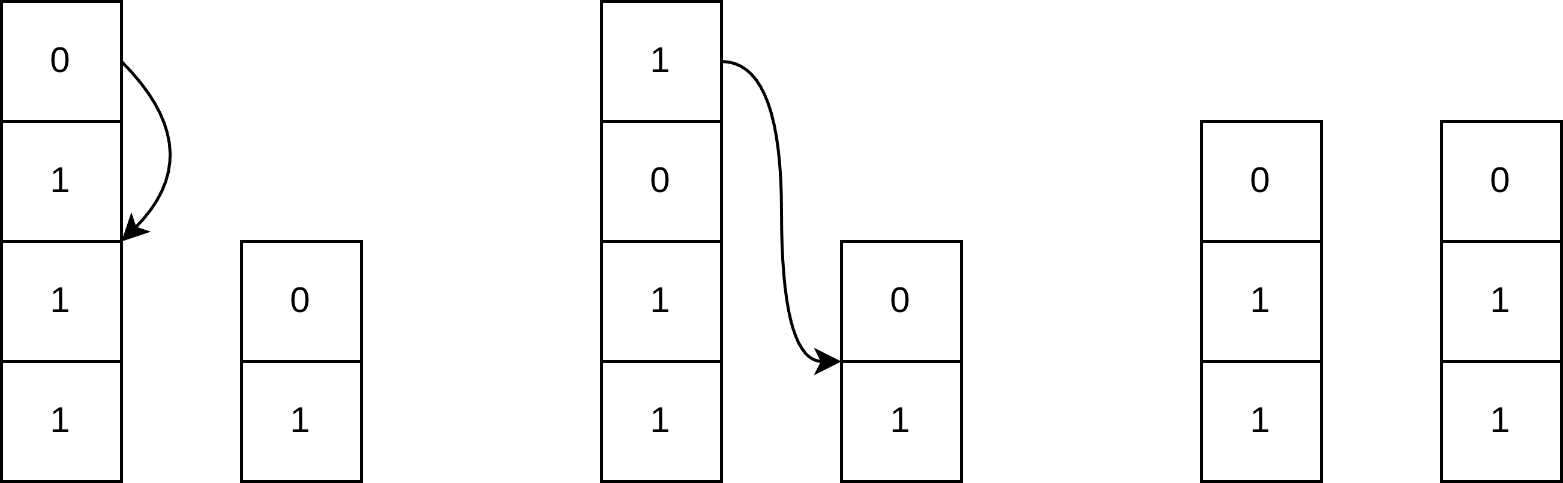
给定 $n$ 个二进制堆，其中第 $i$ 个堆顶部有 $a_i$ 个 $0$，底部有 $b_i$ 个 $1$。 每次操作中，你可以取出任意堆的**顶部元素**，并将其移动到任意堆的任意位置（包括原堆）。  上图为第一个测试样例的解法图示。 计算最少需要多少次操作，才能使第 $i$ 个堆形成顶部 $c_i$ 个 $0$ 和底部 $d_i$ 个 $1$ 的目标状态。

每个测试包含多个测试用例。第一行给出测试用例数量 $t$（$1 \le t \le 10^4$）。随后是各测试用例描述。 每个测试用例第一行包含一个整数 $n$（$1 \leq n \leq 2 \cdot 10^5$），表示堆的数量。 接下来 $n$ 行，第 $i$ 行包含四个整数 $a_i$, $b_i$, $c_i$, $d_i$（$0 \leq a_i, b_i, c_i, d_i \leq 10^9$），分别表示第 $i$ 个堆的初始状态和目标状态。 题目保证存在操作序列可以将所有堆转换为目标状态。 保证所有测试用例的 $n$ 总和不超过$2 \cdot 10^5$。

对于每个测试用例，输出一个整数，表示达成目标状态所需的最少操作次数。

第一个测试用例的解法已在题面中展示。 第二个测试用例的最优解法如下：  第三个测试用例中，所有堆已处于目标状态。